Probabilistic Neural Networks For Gas Turbine Fault Recognition

Introduction

To keep high reliability of gas turbines and reduce maintenance costs, many monitoring and diagnosis systems have recently been developed. Benefits from their application above all depend on the accuracy of diagnostic algorithms constituting the system.

Gas turbine fault identification algorithms based on measured gas path variables (temperature, pressure, rotation speed, fuel consumption, etc.) present an important monitoring system component. With the gas path variables not only gas path abrupt faults and gradual deterioration mechanisms [1] are diagnosed, but also sensor faults [2,3] and control system malfunctions [4] can be identified. The fault identification algorithms widely use the pattern recognition theory. In the last three decades, the use of many recognition techniques has been reported: first of all, Artificial Neural Networks [5-9], but also Bayesian Approach [5,6], Support Vector Machines [7], Genetic Algorithms [10], and Correspondence and Discrimination Analysis [11].

The neural networks present a fast growing technique for gas turbine diagnostics. Among the neural networks, the Multilayer Perceptron (MLP) is the most frequently used technique [9]. Nevertheless, other network type, Probabilistic Neural Network (PNN), is also applied to diagnose gas turbines [3,12,13]. It recognizes (classifies) the faults using the criterion of fault probability. In this way, the PNN has an advantage that every diagnostic decision is accompanied with a probabilistic confidence measure.

The present paper tests the PNN and compares it with the MLP in order to choose the best technique for real gas turbine monitoring systems. To the end of comparison, both networks were included into a special testing procedure. It simulates numerous cycles of the diagnosis and computes for each network an averaged probability of a correct diagnosis (true positive rate). The procedure is realized in Matlab (MathWorks, Inc), which includes a neural networks toolbox that simplifies network creation, training, and use. The procedure was adapted and the calculations of network comparison were made for an industrial gas turbine intended for driving a centrifugal compressor.

The paper is structured as follows. The compared networks are described in Section 1. Next, Section 2 outlines the approach to fault recognition and network comparison realized in the testing procedure. Comparison conditions are then specified in Section 3. Finally, Section 4 presents comparison results.

1. Networks compared

Foundations of the compared networks, MLP and PNN, can be found in many books on recognition theory or neural networks, for example, in [14]. The next two subsections give only a brief network description, which is necessary for better understanding the present paper.

1.1. Multilayer perceptron

The MLP is intended for solving both approximation and recognition (classification) problems. It is a feed-forward network in which signals propagate from its input to the output with no feedback. The structural scheme given in Fig.1 helps to better explain perceptron operation.

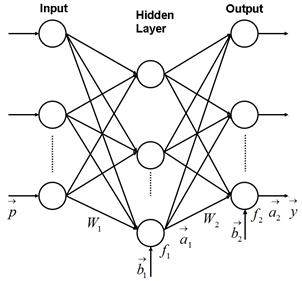
Fig. 1. Multilayer perceptron

The input of each hidden layer neuron is the sum of perceptron inputs (elements of a pattern vector ) multiplied by the corresponding coefficients of a weight matrix W1 with a bias (element of a vector ) added. This neuron input is transformed by a hidden layer transfer function f1 into a neuron output (element of a vector ). Such computation is reiterated for all hidden layer neurons. The perceptron output layer operates in the same way considering the vector  as an input vector. Thus, a network output vector can be given by the expression . When the perceptron is applied to a classification problem, each output yk gives a closeness measure between the input pattern  and a class Dk. The pattern is usually assigned to the closest class and such classification can be considered deterministic.

During the learning, unknown perceptron’s quantities W1, , W2 and  are generally determined by a back-propagation algorithm, in which the network output error is propagated backwards to correct these quantities. They change in the direction that provides error reduction unless the learning process converges to a global error minimum. The back-propagation algorithm needs the transfer functions to be differentiable and usually they are of a sigmoid type.

The other network analyzed in the present paper is a probabilistic neural network (PNN). It differs from the MLP by the application, structure, and the transfer functions employed.

1.2. Probabilistic neural network

The PNN is intended for classification problems. It is a specific type of networks based on radial basis functions. The scheme in Fig. 2 illustrates probabilistic network's operation. Like the perceptron, this network consists of two layers.

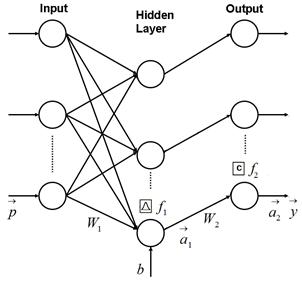
Fig. 2. Probabilistic neural network

The hidden layer (a.k.a. radial basis layer) is quite different from the perceptron’s layers. It is formed in the basis of learning patterns united in a matrix W1. Each learning pattern  specifies a center of a radial basis function (RBF) of one hidden neuron therefore a hidden layer dimension equals a total number of the learning patterns. A neuron input Lj is firstly computed as a Euclidean distance between the function center  and an input pattern . A hidden neuron output  is then calculated through the radial basis function  resulting in . The parameter B called a spread determines an action area of the RBFs. The closer the input vector is situated to the neuron center, the greater the neuron output will be. These outputs, elements of a hidden layer output vector , indicate how close the input vector is to the learning patterns.

For each class the corresponding neuron of the output layer sums the signals  related with the learning patterns of the same class. To this end, a matrix W2 is composed in a particular way from 0 - and 1-elements. A product  is then computed resulting in a vector of probabilities of the considered classes. Finally, the output layer transfer function f2 produces a 1 corresponding to the largest probability, and 0's for the other network outputs. Thus, the PNN classifies the input vector  into a specific class because of its highest probability. Given that this network makes probabilisticrather than deterministic decisions, such classifying is closer to reality than the perceptron-based classifying.

2. Procedure to test and compare the networks

The network testing procedure mentioned in the introduction embraces all the stages of gas turbine fault classification, namely, feature extraction, construction of fault classes, classifying an actual fault pattern, and estimation of classification accuracy. They are briefly described below.

Feature extraction. Some measured variables set a gas turbine operation point and are united in a vector of operating conditions . The rest of measured gas path variables are available for engine condition monitoring and form an (m×1)-vector of monitored variables . Since they much more depend on the operating point than on engine health, not variables themselves but their deviations from an engine baseline  are fault features  to be monitored. In the present study, the faults are simulated and m features

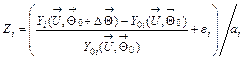  (1)

are computed through a gas turbine thermodynamic model

.                               (2).

The model computes the monitored variables as a nonlinear function of steady state operating conditions and engine health parameters . Nominal values  correspond to a healthy engine whereas changes  called fault parameters slightly shift performance maps of engine modules (compressors, combustor, turbines, etc.) allowing fault simulation. A random error  makes the deviation more realistic and a parameter  normalizes the errors of different deviations simplifying fault class description. The deviations given by expression (1) constitute an (m×1)-vector , which is a pattern to be classified.

Construction of fault classes. For the purposes of diagnosis, numerous gas turbine faults are divided into a limited number q of classes . Each class corresponds to one engine module and is described by its fault parameters , flow parameter and efficiency parameter. Two class types are considered: a class of singular faults is constructed by changing one fault parameter while for a class of multiple faults two parameters of the same module are varied independently. For each class, singular or multiple, numerous patterns  are generated according to expression (1) setting the necessary quantities  and  by the uniform and Gaussian distributions accordingly. A totality Z1 of all classification’s patterns is employed to train the used neural network and is therefore called a learning set.

Classifying fault patterns. In addition to the observed pattern  and the constructed fault classification Z1, a neural network (MLP or PNN) for classifying fault patterns is an integral part of a whole gas turbine diagnostic algorithm. Unknown network coefficients are determined with data of the learning set Z1 as described in Section 1. Once the coefficients have been determined, the network is ready for use, but before real network application it is important to estimate network’s classification accuracy.

Estimation of classification accuracy. To test and validate the network, an additional data sample Z2 called a validation set is created in the same way as the set Z1. The only difference is that other random numbers are generated within the same distributions. The network classifies each pattern of the set Z2, producing the diagnosis dl. Comparing dl with a known class Dj for all validation set patterns, probabilities of correct classification (a.k.a. true positive rates) are estimated for all fault classes. A mean number  of these probabilities determines total accuracy of engine fault classification by the used network. Applying the probability  as a criterion, two analyzed networks, MLP and PNN, are tuned and compared in the sequel.

3. Comparison test case

A gas turbine power plant for natural gas pumping has been chosen as a test case. It is an aeroderivative two shaft engine with a power turbine. In the paper gas turbine diagnosis is analyzed at two operating modes called Mode 1 and Mode 2. They are close to engine maximal and idle regimes and are set in the thermodynamic model by the corresponding gas generator rotation speeds and standard ambient conditions.

Apart from these operating conditions, other 6 gas path variables measured in the power plant are available for monitoring and are used to compute fault patterns. These gas path monitored variables and their normalization parameters ai are specified in Table 1.

Monitored variables           Table 1

№

Variable’s name

ai

1

Compressor pressure p*C

0.015

2

Exhaust gas pressure p*HPT

0.015

3

Compressor temperature T*C

0.025

4

Exhaust gas temperature T*HPT

0.015

5

Power turbine temperature T*LPT

0.020

6

Fuel consumption

0.020

The faults are simulated through 9 fault parameters embedded into the model. As shown in Table 2, faults of four main engine modules (compressor, high pressure turbine, power turbine, and combustion chamber) are described by two parameters and an inlet device is presented by one parameter. Maximal change of each parameter equals 5%.

Fault parameters                Table 2

№

Parameter’s name

1

Compressor flow parameter

2

Compressor efficiency parameter

3

High pressure turbine flow parameter

4

High pressure turbine efficiency parameter

5

Power turbine flow parameter

6

Power turbine efficiency parameter

7

Combustion chamber total pressure recovery parameter

8

Combustion efficiency parameter

9

Inlet device total pressure recovery factor

Two classification variations are considered in the present paper. The first classification embraces 9 single fault classes formed by the parameters of Table 2. The second classification consists of 4 multiple fault classes corresponding to 4 main power plant modules. The class of each module is created by independent variation of two module fault parameters (see Table 2). Regardless of simulated faults, single or multiple, each class is presented by 1000 patterns.

According to the described structures of monitored variables and fault classes, both compared networks have 6 nodes on the input layer and 9 or 4 nodes on the output layer. As to the hidden layer, the PNN have 9000 or 4000 nodes in accordance with the learning set volumes. For the MLP an optimal hidden node number 27 chosen in study [15] is accepted for the present study. Thus, for two classification variations, the MLP structures are written as 6×27×9 and 6×27×4 while the PNN structures are described by 6×9000×9 and 6×4000×4.

4. Comparison results

4.1. Networks tuning

For the sake of correct results each network should be tailored before the comparison. The MLP was tuned for a diagnostic application in our previous works. In particular, a number 27 of hidden layer nodes and a resilient back-propagation training algorithm have been found the best and were accepted for the present study. As to the newly analyzed technique, PNN, its tuning is described below.

Since practically all PNN's coefficients are determined with the learning set data, the only parameter to tailor the network is the spread B (see Section 1). Although Matlab provides an initial value B = 1, it is not obvious that it will be acceptable for the analyzed diagnostic application. That is why the PNN directly applied to gas turbine diagnosis was tailored. Different spread values were employed and the mean probability  (see Section 3) has been computed for each value. It was found that the value ensuring the highest probability depends on classification variation. These values, B=0.35 for the singular fault classification and B=0.40 for the multiple one, were used in the comparative calculations described below.

4.2. MLP and PNN comparison

Two engine operation modes and two classification variations, when changed independently, result in four comparison cases. The network comparison under such different conditions will allow drawing more general conclusions on the networks’ accuracy and applicability.

Within each comparison case the same input data were fed to both networks and the mean probabilities  were computed for each network. Due to a stochastic nature of the computation, these probabilities are known with some uncertainty. Preliminary studies (see, for example, [13]) have shown that the uncertainty interval can be greater than the probability difference for the compared networks. That is why in the present contribution, the probability computation for each comparison case was repeated 100 times, each time with a new seed (parameter that determine a random number series). The obtained probability values are then averaged resulting in an averaged probability . These probabilities computed for the analyzed networks under all comparison conditions are included in Table 3.

Averaged networks diagnostic accuracy   Table 3

(Probabilities  )

Network

Single fault classification

Multiple fault classification

Mode 1

Mode 2

Mode 1

Mode 2

MLP

0.8184

0.8059

0.8765

0.8686

PNN

0.8134

0.8004

0.8739

0.8653

It can be seen in the table that the application of the PNN to gas turbine diagnosis instead of the MLP causes losses of diagnostic reliability for all comparison cases. These losses of the averaged probability  are 0.0050-0.0055 for single faults and 0.0026-0.0033 for multiple faults. It was estimated in [15] that with the confidence of 97.7% an uncertainty interval for  is ±0.00094 (0.094%). Consequently, the observed losses of diagnostic reliability are statistically significant. On the other hand, the observed in Table 3 losses (0.0041 on average) is not too great against the background of total diagnostic inaccuracy (1- ), which is about 0.21 for single faults and 0.13 for multiple faults.

Conclusions

This paper examines the probabilistic neural network in an application to gas turbine diagnosis. To assess diagnostic efficiency and applicability of this network, it is compared with the multilayer perceptron.

A power plant for natural gas pumping has been chosen as a test case. It was presented in the paper by a nonlinear thermodynamic model, with which numerous fault patterns for fault classification were generated.

The networks have been tuned for diagnosing the power plant under analysis. They were then tested under different comparison conditions, using an averaged probability of correct diagnosis as a criterion to choose the best network.

By way of summing up comparison results, the conclusion is that although the perceptron is a little more accurate than the probabilistic network, the latter is recommended for gas turbine diagnosis because it provides confidence estimation for each diagnostic decision, the property very valuable in practice. Thus, the probabilistic neural network can be considered as a perspective technique for real gas turbine monitoring systems. The investigations will be continued to better investigate this new diagnostic technique and to draw a final conclusion on its applicability for gas turbine diagnosis.

Acknowledgments

The work has been carried out with the support of the National Polytechnic Institute of Mexico (research project 20121060).

References

1. Meher-Homji C.B. Gas turbine performance deterioration / C.B. Mejer-Homji, M.A. Chaker, H.M. Motiwala // Proc. Thirtieth Turbomachinery Symposium, Texas, USA, September 17-20, 2001. − P. 139-175.

2. Kobayashi T. Aircraft engine on-line diagnostics through dual-channel sensor measurements: development of an enhanced system /T. Kobayashi, D.L. Simon // Proc. IGTI/ASME Turbo Expo 2008, Berlin, Germany, June 9-13, 2008. − 13 p.

3. Romessis C. Setting up of a probabilistic neural network for sensor fault detection including operation with component fault / C. Romessis, K. Mathioudakis // Journal of Engineering for Gas Turbines and Power. − 2003. − Vol. 125, Is. 3. −P. 634-641.

4. Tsalavoutas A. Identifying faults in the variable geometry system of a gas turbine compressor / A. Tsalavoutas, A. Stamatis, K. Mathioudakis, M. Smith // Proc. IGTI/ASME Turbo Expo 2000, Munich, Germany, May 8-11, 2000. − 7 p.

5. Romessis C. Bayesian Network Approach for Gas Path Fault Diagnosis / C. Romessis, K. Mathioudakis // ASME Journal of Engineering for Gas Turbines and Power. − 2006. − Vol. 128, Is. 1. − P. 64-72.

6. Loboda I. Gas Turbine Fault Recognition Trustworthiness / I. Loboda, S. Yepifanov // Cientifica, Revista del Instituto Politecnico Nacional de Mexico. − 2006. − Vol. 10, Is. 2. − P. 65-74.

7. Butler S. An Assessment Methodology for Data-Driven and Model Based Techniques for Engine Health Monitoring / S.W. Butler, K.R. Pattipati, A.J. Volponi // Proc. IGTI/ASME Turbo Expo 2006, Barcelona, Spain, May 8-11, 2006. − 9 p.

8. Roemer M. J. Advanced Diagnostics and Prognostics for Gas Turbine Engine Risk Assessment / M.J. Roemer, G.J. Kacprzynski //Proc. IGTI/ASME Turbo Expo 2000, Munich, Germany, May 8-11, 2000. − 10 p.

9. Volponi A. J., DePold, H., and Ganguli, R., , “The Use of Kalman Filter and Neural Network Methodologies in Gas Turbine Performance Diagnostics: a Comparative Study / A. Volponi, H. DePold, R. Ganguli // ASME Journal of Engineering for Gas Turbines and Power. − 2003. − Vol. 125, Is. 4. − P. 917-924.

10. Sampath S.Fault diagnosis of a two spool turbo-fan engine using transient data: a genetic algorithm approach / S.Sampath, Y. G. Li, S.O.T. Ogaji, R. Singh // Proc.IGTI/ASME Turbo Expo 2003, Atlanta, Georgia, USA, June 16-19, 2003. − 9 p.

11. Pipe K. Application of Advanced Pattern Recognition Techniques in Machinery Failure Prognosis for Turbomachinery / K. Pipe // Proc. Condition Monitoring 1987 International Conference, British Hydraulic Research Association, UK, March 31 - June 3, 1987. − P. 73-89.

12. Romessis C. Fusion of gas turbine diagnostic inference – the Dempster-Schafer approach / C. Romessis, A. Kyriazis, K. Mathioudakis //Proc. IGTI/ASME Turbo Expo 2007, Montreal, Canada, May 14-17, 2007. − 9 p.

13. Estrada Moreno R.Redes Probabilísticas Enfocadas al Diagnóstico de Turbinas de Gas / R. Estrada Moreno, I. Loboda // Memorias del 6to Congreso Internacional de Ingeniería Electromecánica y de Sistemas, ESIME, IPN, México, D.F., 7-11 noviembre de 2011. − P.63-68.

14. Duda, R.O. Pattern Classification / R.O. Duda, P.E. Hart, D.G. Stork. − New York: Wiley-Interscience, 2001. − 654 p.

15. Loboda I. Neural networks for gas turbine fault identification: multilayer perceptron or radial basis network / I. Loboda, Ya. Feldshteyn, V. Ponomaryov // International Journal of Turbo & Jet Engines. − 2012. − Vol.29, Is. 1. − P. 37-48.