Verification of a Gas Turbine Model
Abstract — Identification of a gas turbine thermodynamic model may be interpreted as an inverse problem and therefore is potentially unstable. Regularization is a common principle to make a solution of any mathematical problem more robust to possible input data perturbances. In this paper with a purpose of diagnostic application, we propose a regularizing algorithm of gas turbine model identification. To verify the developed software, choose a proper regularization degree and determine averaged accuracy indicators, the algorithm is put to the statistical testing. The results obtained on both simulated and real input data show that the algorithm has certain advantages and can be constructed and work successfully in gas turbine operating health monitoring systems.
Key words — Accuracy indicators, Gas turbine thermodynamic model, Model identification, Regularization, Statistical testing
I. INTRODUCTIONGas turbine mathematical models based on a well developed theory of gaspath flow are widely used either in an engine design or in its control and monitoring system development. Model application not only contributes to reducing the development funds and time, but also can provide new information about a gas turbine state and behavior. In such models, a lot of the gaspath variables (flow pressures and temperatures, rotor speeds and many others) are computed as functions of gas turbine operational conditions (control variables such as the fuel consumption and ambient conditions: total inlet pressure and temperature) and engine state parameters (correction factors for performances of every component: compressors, turbines, combustion chamber etc.). In general these functional dependencies are non-linear.
Component performance maps (for example, dependencies of the compressor efficiency and pressure ratio from the air flow and rotation speed) included in the calculations are known with certain unauthenticity as a rule. Moreover in maintenance, the performances are changed due to contamination, erosion and other negative processes in engine. For this reason, the thermodynamic models often include special internal parameters (correction factors, state parameters) which permit to displace original performance maps and, in this way, take in consideration an actual engine state.
To fit the thermodynamic model to gaspath measured variables, model identification tools are applied which determine such values of the state parameters which minimize the distance between simulated and measured variables. In addition to common enhancement of model accuracy, the model identification provides valuable diagnostic information as the found correction factors help to determine health of every component. Along with advances in instrumentation and computer technology, an application of identification tools becomes more widespread in gas turbine health monitoring and diagnostics [1-3].
Proceeding with our work on model identification [4-6], this paper proposes and examines a regularizing algorithm of the thermodynamic model identification. The main focus is to evaluate identification accuracy under different conditions of the algorithm functioning and give recommendations of its practical application for a gas turbine diagnosing.
II. Thermodynamic model
The thermodynamic model is intended for calculating the gaspath variables
![]() on gas turbine steady state operational regimes given by a vector
on gas turbine steady state operational regimes given by a vector
![]() of control variables and ambient conditions. Additionally, gas turbine health changes are taken in account by introducing a vector
of control variables and ambient conditions. Additionally, gas turbine health changes are taken in account by introducing a vector
![]() of correction factors. Thus, the thermodynamic model can be presented by a nonlinear vector function
of correction factors. Thus, the thermodynamic model can be presented by a nonlinear vector function
![]() . (1)
. (1)
In a successive calculation of gaspath variables, some of them are unknown and may be determined only as a result of combined work of all engine components. For this reason, the thermodynamic model is organized as a system of nonlinear algebraic equations resolved numerically by the Newton-Rafson method.
Software of the nonlinear model permits to calculate a linear model
![]() , (2)
, (2)
which connects small changes of state parameters
![]() and gaspath variables
and gaspath variables
![]() by an influence matrix H for fixed operational conditions. As will be shown below, linear model calculation is an integral part of an identification procedure.
by an influence matrix H for fixed operational conditions. As will be shown below, linear model calculation is an integral part of an identification procedure.
III. Base identification procedure
Mathematically, the identification of the model (1) on the measurements
![]() and
and
![]() presents an optimization problem
presents an optimization problem
![]() , (3)
, (3)
where
![]() means a vector norm.
means a vector norm.
To estimate q parameters
![]() , a number m of measured parameters must be equal or greater. Usually in order to enhance accuracy of the estimations, the measurements are collected on N different operational regimes and a generalized discrepancy vector
, a number m of measured parameters must be equal or greater. Usually in order to enhance accuracy of the estimations, the measurements are collected on N different operational regimes and a generalized discrepancy vector
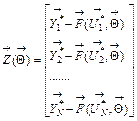 . (4)
. (4)
is to be minimized.
In an actual iteration n of the identification procedure, a correction
![]() to a nonlinear solution is found as a solution of a linear system
to a nonlinear solution is found as a solution of a linear system
![]() , (5)
, (5)
where
![]() is a generalized influence matrix compounded from elemental matrixes calculated for every identification regime.
is a generalized influence matrix compounded from elemental matrixes calculated for every identification regime.
Applying the described identification procedure, we sometimes encountered that absolute values of the estimations
![]() were too great. Such estimations could not be accepted as physically correct; moreover they provoked halts of a running identification program. The main cause is that some columns of the matrix H are almost lineally dependent. The additional factors are a lack of input information – measured gaspath variables
were too great. Such estimations could not be accepted as physically correct; moreover they provoked halts of a running identification program. The main cause is that some columns of the matrix H are almost lineally dependent. The additional factors are a lack of input information – measured gaspath variables
![]() – and exceeded number of the estimated parameters
– and exceeded number of the estimated parameters
![]() . The explained reasons make the model identification to be an ill-conditioned problem inducing unstable estimations.
. The explained reasons make the model identification to be an ill-conditioned problem inducing unstable estimations.
Regularization is a general principle to prevent such a difficulty that means imposing restrictions on sought quantities during estimating. In the next section, we show how the non-regularizing identification procedure described above can be modified to be a regularizing one.
IV. Regularizing identification procedure
One of the general modes to regularize a solution is extension of the minimized functional (see expression 3) by a solution norm as follows
![]() , (6)
, (6)
where
![]() is a weighting coefficient.
is a weighting coefficient.
To realize the problem (6) algorithmically, the vector
![]() and matrix
and matrix
![]() must be structurally modified according the following expressions
must be structurally modified according the following expressions
 (7)
(7)
and
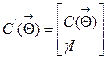 . (8)
. (8)
As can be seen in expression (6), an regularizing effect of the coefficient
![]() depends on norms of the discrepancy vector and estimation vector and consequently on the identification conditions m, N, r. To make this effect more independent, a regularization parameter
depends on norms of the discrepancy vector and estimation vector and consequently on the identification conditions m, N, r. To make this effect more independent, a regularization parameter
![]() is introduced by a formula
is introduced by a formula
![]() (9)
(9)
to be used below.
It is clear that the proposed regularizing identification procedure retains the option of non-regularized estimations when
![]() =0.
=0.
As every newly developed program, the regularizing procedure should be thoroughly tested. For this reason, we organized three stages of testing: 1) on simulated input data without a noise of measurement, 2) on simulated input data with the noise, 3) on real input data.
The simulated gaspath variables were generated by the thermodynamic model of a two shaft turbofan with introduced changes of state parameters
![]() .
.
The most common conditions of the model identification on simulated data were: standard day conditions, five measured parameters, 12 operational regimes, 17 values of the regularization parameter (α=0, 0.001, 0.003, … , 1.0), 1-2 simulated parameters
![]() , 2-4 estimated parameters
, 2-4 estimated parameters
![]() .
.
V. Testing on simulated data without noise
The base identification procedure was well tested during along period of previous use. On the other hand, the changes in the new procedure were only related with introducing the regularization. That is why, our nearest objectives were to compare the old and new procedures under the condition
![]() =0 and to verify a regularization effect on the new procedure.
=0 and to verify a regularization effect on the new procedure.
Executing the regularizing procedure with
![]() =0, it was stated that the identification process and resulting estimations
=0, it was stated that the identification process and resulting estimations
![]() completely coincide with the work and results of the original procedure.
completely coincide with the work and results of the original procedure.
The results of the model identification with the variable regularization parameter have shown (see Fig.1) gradual growth of the discrepancy
![]() and reduction of the estimation norm
and reduction of the estimation norm
![]() along with augmentation of
along with augmentation of
![]() that agree with theoretical ideas of regularization influence.
that agree with theoretical ideas of regularization influence.
These calculations with variable
![]() helped us to assess a possible degree of regularization: restricting an estimation shift by 10% we established that the parameter
helped us to assess a possible degree of regularization: restricting an estimation shift by 10% we established that the parameter
![]() should be less than 0.03. However, final decision about optimal value of the regularization parameter can be made taking into account not only the shift but also an estimation scatter. The last can be found by a statistical testing of the analysed procedure when the input data contain random errors (noise).
should be less than 0.03. However, final decision about optimal value of the regularization parameter can be made taking into account not only the shift but also an estimation scatter. The last can be found by a statistical testing of the analysed procedure when the input data contain random errors (noise).
VI. Testing on simulated data with noise
To determine better a distribution, mean number and dispersion of the estimations
![]() , the identification is repeated numerously on simulated gaspath variables obtained in the same operational conditions and contained different normally distributed measurement errors. A testing cycle number 1000 was accepted which ensured a high accuracy of 0.02% for gaspath variables and 0.05% for state parameters and required a moderate computer time of 20 minutes (Pentium IV, 2.6GHertz).
, the identification is repeated numerously on simulated gaspath variables obtained in the same operational conditions and contained different normally distributed measurement errors. A testing cycle number 1000 was accepted which ensured a high accuracy of 0.02% for gaspath variables and 0.05% for state parameters and required a moderate computer time of 20 minutes (Pentium IV, 2.6GHertz).
With this cycle number and different regularization parameters, two calculation series were made: in the first, two state parameters were estimated (parameter
![]() of a compressor map displacement along its consumption axis and
of a compressor map displacement along its consumption axis and
![]() - the displacement along the efficiency axis) and, in the second, four parameters (
- the displacement along the efficiency axis) and, in the second, four parameters (
![]() ,
,
![]() ,
,
![]() - a turbine map displacement along its consumption axis and
- a turbine map displacement along its consumption axis and
![]() - the displacement along the efficiency axis). The simulated values were
- the displacement along the efficiency axis). The simulated values were
![]() =-0.03 and
=-0.03 and
![]() -0.04.
-0.04.
As the results of the first series of calculations showed, the distributions were close to the normal and the regularization shifted the mean values of the estimations leaving the distributions and dispersions without of a visible change.
In the second series, the estimations
![]() and
and
![]() conserved the described properties but the estimation
conserved the described properties but the estimation
![]() and
and
![]() have changed the behaviour. As can be seen in Fig.2, the distributions are non-symmetric at the small regularization parameter
have changed the behaviour. As can be seen in Fig.2, the distributions are non-symmetric at the small regularization parameter
![]() =0.01, the dispersions are great and the mean values are close to the simulated values. Increasing the parameter up to
=0.01, the dispersions are great and the mean values are close to the simulated values. Increasing the parameter up to
![]() =0.04 radically changed the estimations: the distributions approached to the normal one, the dispersions decreased considerably and the mean values were shifted. Such a different behavior of the estimations
=0.04 radically changed the estimations: the distributions approached to the normal one, the dispersions decreased considerably and the mean values were shifted. Such a different behavior of the estimations
![]() and
and
![]() is explained by the mentioned before lineal dependency between their columns in the influence matrix H. In addition to a positive effect of the scatter reduction, the regularization application made the identification procedure much more stable, for example, an unavailable earlier case of eight estimated parameters became possible to calculate.
is explained by the mentioned before lineal dependency between their columns in the influence matrix H. In addition to a positive effect of the scatter reduction, the regularization application made the identification procedure much more stable, for example, an unavailable earlier case of eight estimated parameters became possible to calculate.
To sum up the results of testing on simulated data, it can be previously stated that the regularization can be usefully applied in the gas turbine model identification, however, a level of the regularization should be limited.
To verify more a regularization effect, the proposed identification procedure was tested on real data.

Fig.1 Influence of the regularization on mean values
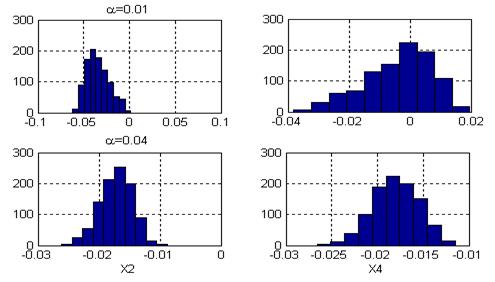
Fig.2 Estimation distributions (four estimated parameters)
VII. Testing on real data
We proposed earlier [4] to divide registered maintenance data on successive samples, identify the thermodynamic model on every data sample and analyze a diagnostic value (failure induced systematic changes against a background of random errors) of a series of the corresponding successive estimations
![]() plotted vs. time variable. Waiting for enhancement of such series, in this paper we apply the regularizing identification procedure to the same maintenance data.
plotted vs. time variable. Waiting for enhancement of such series, in this paper we apply the regularizing identification procedure to the same maintenance data.
The data and the thermodynamic model are used of a two shaft free turbine power plant to drive a gas pumping unit. A total data set incorporates 3880 points of the variables
![]() and
and
![]() registered every hour. The analyzed set includes two periods of a compressor contamination and a compressor washing between them and therefore presents interesting information for diagnostics. The set was divided into 97 data samples of 40 points and 97 corresponding estimations
registered every hour. The analyzed set includes two periods of a compressor contamination and a compressor washing between them and therefore presents interesting information for diagnostics. The set was divided into 97 data samples of 40 points and 97 corresponding estimations
![]() were computed by the identification procedure. The calculations were repeated for every value of the regularization parameter. So, it became available to consider a regularization effect on real data.
were computed by the identification procedure. The calculations were repeated for every value of the regularization parameter. So, it became available to consider a regularization effect on real data.
Fig.3 and Fig.4 demonstrate time plots of the estimations
![]() and
and
![]() correspondingly. It can be seen that the estimations correctly reflect influence of the washing (in the point 23) and contamination before and after the washing. In relation to the regularization, it does not make worse the diagnostic value at least. On the contrary, the plots corresponding to a great regularization level (
correspondingly. It can be seen that the estimations correctly reflect influence of the washing (in the point 23) and contamination before and after the washing. In relation to the regularization, it does not make worse the diagnostic value at least. On the contrary, the plots corresponding to a great regularization level (
![]() =0.2) have become more informative.
=0.2) have become more informative.
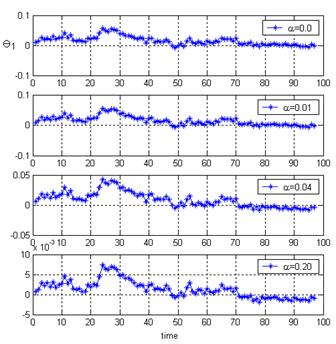
Fig.3 Regularization influence on successive
estimations
![]()
Conclusions
In summary, the most important results of the paper are as follows.
Verifying the proposed regularizing procedure for a gas turbine model identification and comparing it with the base identification procedure, we have demonstrated that the proposed procedure operates correctly in all conditions of the verification.
The further statistical testing on simulated data has shown that the regularization of the estimated state parameters makes the identification procedure more
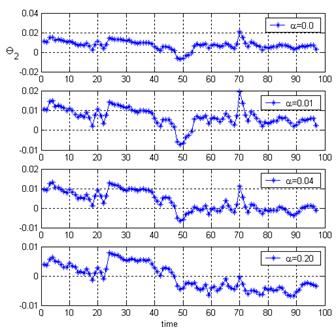
Fig.4 Regularization influence on estimations
![]()
stable and reduces estimation scatters. On the other hand, the regularization shifts mean values of the estimation and should be applied carefully. In the conditions of fulfilled calculations, the values 0.02-0.03 of the regularization parameter can be recommended.
Sampling the proposed procedure on real data has justified that the regularization of the estimations can enhance their diagnostic value.
Acknowledgments
The work has been carried out with the support of the National Polytechnic Institute of Mexico (project 20050709).