Loboda Igor

Deviation Problem In Gas Turbine Health Monitoring

ABSTRACT

This paper looks at the deviations forming as differences between actual measurements and a normal state function for further application in gas turbine monitoring, diagnostics, and forecasting. The focus of the paper is possible greatest reducing the deviation random errors in order to observe more clearly the trends and to detect corresponding gas turbine faults. Possible error sources are examined and some methods are proposed to enhance the normal function and the deviations. Real maintenance data and gas turbine nonlinear thermodynamic model are applied to realize and verify these methods.

1.  Introduction

Gas turbine based combined cycle plants will be the dominant of power generation for the next several decades. These plants are characterized by large capital investment and high fuel costs and, therefore, need for health monitoring in order to minimize risk and the economic impact of an unexpected shutdown or failure. Therefore, usage of health (condition) monitoring systems becomes standard [1-3]. Some organizations have reported 30% maintenance saving due to implementation of the condition monitoring program [4].

The monitoring algorithms analyzing registered gaspath variables (pressures, temperatures, air-gas flow rate, rotation speeds, fuel consumption, and any others) provide invaluable insight into gas turbine operating health. Besides the gaspath failures (for example, gradually developed compressor blade contamination, aerodynamic surfaces distortion, and seal wear), control system and measurement system malfunctions can be also detected.

To produce a final diagnostic decision the raw measurement data are subjected to a complex mathematical treatment including a stage of the deviations computing [1,3,5]. The deviations are calculated as discrepancies between measured gaspath parameters and any normal state function built for a healthy gas turbine. In contrast to the same measured parameters, in which fault effects are hided by influence of inlet and control conditions (atmospheric pressure and temperature, engine control system variable, such as fuel consumption), their deviations are free of this influence and may serve as good health indicators. However, a lot of negative factors affect the deviation accuracy masking fault effects and reducing final diagnostics reliability.

Presented paper generalizes our previous experience of a deviation problem analysis [6,7] and also describes new studies. As opposed to the mentioned works [1-5], this paper is concentrated on detailed analysis of deviation accuracy.

2.  Deviation error problem

Experimental variable registration during the operation of the gas turbine driven a natural gas compressor unit is used as a source of real data. In the used database smoothing of and filtered parameter values were registered by an automated diagnostic system within an hour interval. Registration covers the period of axial compressor fouling and subsequent cleaning that presents important information for the diagnostics because the fouling can be recognized as one of the most frequent gas turbine faults [8]. To analyze deviation time plots, deviation quality may be defined as an accompanying factor of systematic changes induced by the fouling in background of random errors.

Fig.1 demonstrates the deviations δY* (%) for the parameters of compressor pressure РC and turbine temperature ТТ  plotted versus power plant operation time t. The deviation is determined here as a relative discrepancy between the measured parameter  and its normal state function :

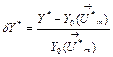,                           (1)

where   is the vector of inlet and control measured parameters chosen as normal function arguments. Numerous function variants were generated and deviations are built and compared to choose the best function that corresponds to the presented deviations.

It may be concluded about deviation behavior in Fig.1 that a compressor washing (t = 7970h) and previous subsequent fouling are well illustrated, however the fluctuations are still significant and capable to mask the failure effects.

With the object of detailed fouling diagnostics, the axial compressor performance parameters (efficiency and flow rate) as well as other components performances were estimated on the same data  and  by means of the identification procedure of nonlinear thermodynamic model [7]. All registered data were divided into subsequent time portions, the model was repeatedly identified on every portion, and corresponding efficiency and flow rate estimations were obtained and plotted at time. It was concluded from the plot observations that the estimations correctly reacted upon the fouling and washing, however the errors had been increased compare to the measured parameter errors. It was also clear that estimation errors are induced by the fluctuations in discrepancies between the model and measured gas path parameters. Consequently, identification accuracy and final diagnostics trustworthiness directly depend on deviation quality.

3.  Deviation error structure

For detailed error problem analysis, the deviation characteristics are introduced as it is shown in Fig.2. The systematic influence of compressor fouling on gas turbine parameters is well known [9, 10] and corresponds to the bold line with maximum change designated as . The fluctuations may be characterized by the mean or maximum error δ and conditionally separated according to a frequency and amplitude into three levels:  1) observed in every calculated point high frequency noise of the maximum amplitude  < 0.3%, 2) more slow fluctuation for the period of 30-300 hours and the amplitude < 1.5%, 3) single jumps  > 1.5%. The relative error  can serve as a index of deviation diagnostic quality. Random measurement errors inside of acceptable bounds cause the fluctuations  which do not present any obstacle in correct diagnosing in contrast to the fluctuations  and  which had to be removed or possibly reduced.

Analyzing a structure of the formula (1) the following components of the total deviation error  can be picked out:

-  - component induced by measurement errors of the same parameter ;

-  - component provoked by a systematic error of the normal function ;

-  - component induced by measurement errors of the function arguments ;

-  - component related with a possible absence in function structure any additional inlet and control parameters  that affect the gas turbine behavior but still can not be chosen as the arguments.

Taking into account the listed components the deviations will view as follows:

,        (2)

where  is a systematic discrepancy due to changes of gas turbine state.

4.  First results of deviation plot analysis

How could be detected the error sources? The question is not trivial because they act together and a total error is comparatively small (about 1%). Knowledge of particular error component behavior assists to understand its cause and source.

The components  of different parameters  can be considered as independent and the corresponding fluctuations in its plots – no simultaneous. The components may be both independent and correlated because some common factors affect the normal function accuracy. The fluctuation components  and  have to be simultaneous due to a common character of argument influence.

Developed graphical tools of the diagnostic system promote a successful exploration of abnormal deviation behavior. General graphical modes applied to deviation analysis are:

- time plot of some deviations “Deviation 1, Deviation 2, …, versus Time”;

- one deviation as a function of another “Deviation 1 versus Deviation 2”;

- time plot of any deviation and some arguments “Deviation 1, Argument 1, Argument 2,…, versus Time”;

- time plot of parallel measurements of the same parameter or closely connected parameters  and .

For special cases, more complex graphs were plotted and theoretical analysis was applied to verify hypothesis of deviations abnormal fluctuation. Application of such a graph-based approach permitted to fix the following malfunctions of measurement and control systems:

- single measurement failures in  missed by the filtration algorithms, that provoked the deviation jumps of 2-5%;

- multiple failures in ambient temperature tH measurement, that induced pulses in all deviations; the parameter tH has been exchanged in the normal function on the parameter tin of inlet temperature;

- periods of abnormal functioning of the sensor tin after the time 11350; corresponding fluctuations are well observed in Fig.1;

- control malfunctions of inlet variable vanes.

Additionally, the gas turbine warming-up effect was observed in the form of deviation variations during 10-15 minutes after an operation regime change. This became a reason to introduce a half hour registration delay that eliminates influence of such a transient process on collected data.

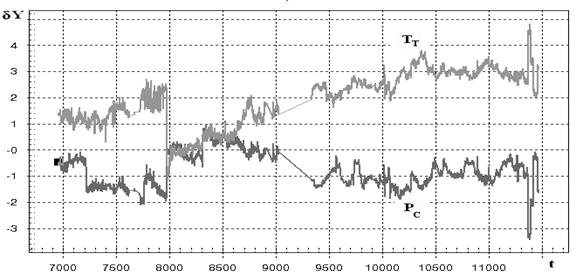
Fig.1. Database deviations

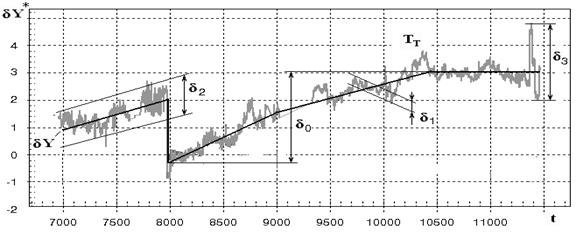
Fig.2. Deviation characteristics

One more source was determines, a normal function non-adequacy. A variable distance among the function and measured data generated deviation shifts every time when the operation regime was changed. So, the function structure and computational method have to be considered and enhanced.

5.  Normal state function

It is known the gas turbine power and climatic curves are smooth and well described by polynomials, therefore they have been accepted for the state norm.

The list of arguments includes: a) one of the main regime parameters, for instance, fuel consumption Gf; b) additional power turbine regime parameter, generally, shaft rotation speed npt; c) air inlet temperature Tin; d) ambient air pressure PH.

Chosen as basic the second order full function of four mentioned arguments includes 15 items:

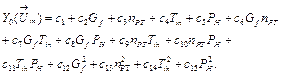(3)

To find the unknown coefficients ci a learning sample is formed as a fragment of the mentioned above database, and the least square method approximation is applied. The found function is verified by means of the deviation computation on a testing sample which, in general, incorporates all available data.

The described algorithm operates in the programming environment Matlab that simplifies visualization and necessary multiple modifications.

First of all, two obvious ways to enhance the function were examined: a) relative form of the function and arguments, b) third order polynomial. However this ways had no any positive effect, the function accuracy and deviation quality left practically the same. Probable explanations are, in the first case, high accuracy of the Matlab operations with double precision variables and, in the second case, adequacy of the second order polynomials for gas turbine behavior.

Secondly, the learning sample problem was concerned that seems as challenging. On the one hand, to satisfy approximation requirements, the learning sample must be representative and incorporate data collected in all passable operation regimes and at different ambient conditions. On the other hand, equipment technical conditions do not permit arbitrary regime changes; moreover, data collection period is limited by a short time when a gas turbine state can be considered as invariable. As a result, the normal function is not adequate in the operation where points of the learning sample were absent. For this reason, the stage of normal function adjustment was long and complicated.

Two described below methods overcome mentioned difficulties. In the first, the thermodynamic model is applied.

6.  Model-based normal function

The thermodynamic gaspath model  relates the gaspath parameters  with the inlet and control parameters  and special internal parameters - corrections factors , which are able to displace the gas turbine component performances and by such a mode to adjust the model to real data. The model software includes a description of gaspath thermodynamic processes and conditions of the component combined work on steady-state regimes and presents a complex calculating procedure.

The model  adjusted to the data of a normal gas turbine state may be used as a normal function to build the deviations. In contrast to a formal polynomial function, such a physical model conserves its correct behavior in all regions of argument space. However, the model is critical to computer time and is not so flexible to follow all real data changes including small ones.

For this reason, the thermodynamic model was introduced to form a learning sample only and kls=330 points were generated uniformly in the argument space as distinct from all database points located into two small regions only. The proposed approach has provided the positive results: calculated deviations (Fig.3a) have at least the same quality as the database ones (Fig.1). Moreover, the experiments show that the model-based function excels in quality all function variants with the same volume kls of database learning sample.

7.  Function with a fouling argument

The other method to form a learning sample consists in introducing a fouling variable uf into the vector  of normal function arguments in order to relate all time dependent changes in learning sample data  with this argument and to avoid their influence on other function items. Such a function has not any restriction on the time interval to form the sample and a lot of registered data can be included. Later, to transform the described function with calculated coefficients into the normal function the argument uf should be removed.

Fouling effect on the gaspath parameters (bold line in Fig.2) served as information to determine the argument uf in the learning sample. The sample included 2608 database registered points with no fragments of displayed measurement problems. The deviations constructed in the described conditions have been demonstrated the further normal function enhancement. However, the method is not devoid of limitations: it needs a priory quantitative information about the fouling. That is why the modernization is concerned to use the time variable t directly instead of the fouling variable.

The next study consists in a choosing the best regime parameter for the normal function.

8.  Selection of regime parameter

Universal form of the deviation calculation algorithm allows changing a normal function argument by a simple indication of the parameter number in a total parameter list. That is why all possible variables were examined. At the first glance, the variable nhp of high pressure rotor speed measured with high accuracy could be the best regime parameter.

Table 1 contains the errors  of every deviation and their mean number presented for all regime variables and ranged according to this mean number. The learning sample included 2608 points mentioned above. From Table 1 it can be seen the parameters nhp and Gf are situated in the low part of the table and the parameter TT occupies the first place. The explanation is that regime parameter quality depends not only on its measurements errors, but also on its influence on the gas turbine behavior which is great for the parameter nhp.

Table 1. Deviation errors for regime parameter variants

Vari ant	Deviations
TТ	TPT	PC	PТ	Gf	TC	nhp	Nе	mean
TТ	-	0.12	0.07	0.08	0.13	0.12	0.39	0.17	0.108
TPT	0.18	-	0.11	0.11	0.17	0.11	0.13	0.15	0.127
PC	0.08	0.08	-	0.66	0.18	0.45	0.17	1.20	0.141
PТ	0.09	0.08	0.74	-	0.16	0.92	0.19	6.11	0.143
Gf	0.12	0.10	0.15	0.16	-	0.67	0.31	0.51	0.157
TC	0.12	0.08	0.36	0.33	0.86	-	0.27	1.10	0.167
nhp	0.35	0.14	0.19	0.21	0.36	0.26	-	0.29	0.216
Nе	0.17	0.11	1.42	1.69	1.01	1.41	0.25	-	0.224

9.  Achieved accuracy level

As it is clear from above explanations, the best achieved deviation quality corresponds to the case of the fouling variable involving and the turbine temperature selecting as a regime parameter. For such a variant, every deviation may display the fouling development and the achieved accuracy level. However, the idea appears to calculate a mean deviation to reduce random fluctuations.

Taking into account the fouling influence on deviations for regime parameter TT the mean deviation formula

          (4)

has been composed from the four best particular deviations. The deviation  plotted in Fig.3b has demonstrated the higher accuracy than any of its components. It seems to be a perfect index of the compressor fouling development and, in general, of any other changes of gas turbine technical condition.

The plot in Fig.3b also shows the remaining fluctuations; therefore common factors, which affect all particular deviations, still exist. Taking into account the above analysis these fluctuations can be classified as errors  and the range of the affecting factors can be narrowed. Such probable factors are: a) ambient air humidity influence, b) gas turbine case variable temperature that causes turbine tip clearance variations and corresponding turbine performance changes, c) compressor control malfunctions, d) fuel natural gas variable calorific value.

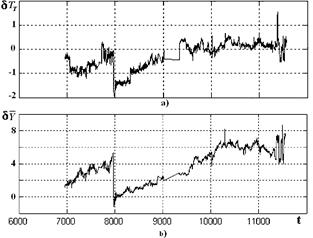
Fig.3. Deviations

а)  deviation for the regime parameter Gf;

b) mean deviation for the regime parameter TT

The reached accuracy is already sufficiently high and is not inferior to the level known from the literature [for example, 1,3,9]. That is why, the further progress will not come easily.

For instance, there is a possible cause of the fluctuation - the fouling development itself. According to the formula (1), the deviations will be constant for different operation regimes if the changes in gaspath parameters induced by the fouling are strictly multiplicative. Otherwise, the fouling will produce a deviation shift for every regime variation.

To simulate the fouling, the compressor performance was corrected and gaspath parameters were calculated before and after the fouling on 5 different regimes for 2 regime parameters nhp and Gf. Table 2 provides the results, where  - minimum deviation for all regimes,  - maximum deviation,  - deviation maximum difference. Analyzing the table it becomes clear that the fouling generally has a multiplicative character, however, it can provoke deviation fluctuations about 0.5% that can not be considered as an inessential factor.

Table 2. Deviations on different regimes

	PC	PТ	TC	TТ	Gf	nhp
nhp – const
	-.0370	-.0384	.0006	0	-.0371	-
	-.0360	-.0341	.0012	.0038	-.0316	-
	.0010	.0043	.0006	.0038	.0055	-
Gf  - const
	-.0181	-.0189	.0073	.0145	-	.0048
	-.0163	-.0154	.0102	.0172	-	.0093
	.0018	.0035	.0029	.0027	-	.0045

Is the achieved deviation accuracy sufficient for a successful gas turbine diagnostics? To answer this question the deviations δY* were used in order to estimate corrections to the compressor maps and plot them in the time. As it can be seen in Fig.4 the air flow and efficiency corrections properly reflect a systematic influence of the compressor fouling and washing in the background of random errors. So, the achieved deviation accuracy is sufficient for gaspath problem detection.

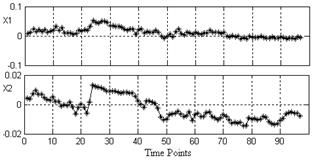
Fig.4. Compressor map corrections

(X1 - air flow corrections, X2 – efficiency corrections, clearing corresponds to the point 23)

10.  Conclusion

Thus, the deviation formation, which presents an important problem of gas turbine monitoring, diagnostics, and forecasting, has been concerned in this paper. The normal state polynomial function was examined and used for the deviation computing; three methods to build the function and the criterion of the fouling development have been proposed and verified on real data. The gained experience is planned to be used for an enhancement diagnostic algorithms based on the thermodynamic model. The described results can be also applied for a measurement system modernization.

11.  Acknowledgments

The work has been carried out with the support of Compressor Controls Corporation, Iowa (U.S.A.) and National Polytechnic Institute of Mexico (project 20040405).