Loboda Igor

Trustworthiness Problem Of Gas Turbine Parametric Diagnosing

Abstract

In the paper, different gas turbine parametric diagnosing methods are analyzed on the base of trustworthiness criteria. The nonlinear gaspath thermodynamic models, random number generators, and real registration data are used for methods adjustment and verification. The achieved trustworthiness level is sufficient to recommend the examined methods for realization in automated diagnosing systems.

1. INTRODUCTION

Modern gas turbine engines represent powerful and efficient sources of mechanical energy for numerous industry branches and transport objects. For a gas turbine which is considered as a complex and expensive system, there is a tremendous benefit of extending the time between overhauls and reducing the probability of a failure in the field. Key factor to the useful life extending is the capability to extract information to produce accurate diagnostics and prognostics about the system state.

The algorithms of gas turbine failure detection which analyze registered gaspath parameters (pressure, temperatures and consumptions of the gas flow, rotation speeds, fuel consumption, and any others) may be considered as principal algorithms of the automated diagnosing system. Besides the gaspath failures, for example, gradually developed compressor blade contamination, aerodynamic surfaces distortion, and seal wear, control system and measurement system malfunctions can be also detected analyzing gaspath parameters.

To produce the final diagnosing decision the raw measurement data are subjected to a complex mathematical treatment and a lot of negative factors affect the resulting trustworthiness. That is why the total diagnosing system effectiveness principally depends on its trustworthiness characteristics and this is a reason to carry out the investigations in this direction. Considerable benefits may be reached from such studies especially if this work precedes the diagnosing system maintenance stage.

2. MODELS APPLIED

Mathematical models of different types are widely used in diagnosing process due to an infrequent display of gas turbine failures, high cost of physical failure modelling, and other causes. The following types of diagnostic gaspath models were used in the fulfilled investigations: nonlinear and linear static and nonlinear dynamic models.

Static multi-regime nonlinear thermodynamic model can be presented by the common expression , where the vector  of gaspath parameters depends on the vector of engine regime and atmospheric conditions  and the vector of state parameters  used for describing the engine failures. Gas turbine component performance parameters are chosen as the state parameters; these performance parameters are able to displace component performances and simulate the failures by this mode. The nonlinear model parameters  are computed numerically as a solution of the system of algebraic equations reflecting the conditions of the components combined work on steady-state regimes.

The linear model  connects the small relative deviations d of state parameters with the relative deviations  of gaspath parameters by means of the matrix of influence coefficients Hon a constant chosen operational regime.

A modification of the static model equations to the conditions of transient regimes permits to form a dynamic model , where the vector of regime and atmospheric conditions , in contrast to the static model, is given as a function of time, and a separate influence of the time variable t is explained by an inertia nature of gas turbine dynamic processes.

Let us consider that the models adequately describe the object, the model generated values  differ from the measured ones  due to the random measurement errors  only, and .

The models may be fitted to real data by means of identification procedures which look for the state parameter estimations  minimizing the error level and carrying the diagnostic information of engine current state.

3. DIAGNOSING METHOD GROUPS

It is supposed in the pattern recognition theory that an object may belong to one of q determined beforehand classes D1, D2, …, Dq  only. Various types of gas turbine classifications exists; in this paper a class is determined as a failures totality of corresponding engine component.

Let us name the space  in which the classes are formed and the diagnosing decision is taken as a diagnostic space. Depending on a type of the diagnostic space, numerous failure detection methods may be united into two main groups.

Methods of the group 1 (for example, Roemer and Kacprzynski, 2000). The diagnostic space is congruent with the space of measured parameter deviations: . For methods of this group there is a theoretical possibility to form the classification on real data and eliminate the models (and their inaccuracy) from the diagnosing process that promises a significant engine controllability growth. On the other hand, the available real information generally is not sufficient and the models are involved in the class formation. Additionally, rigid class boundaries make difficulties for the diagnosing of complex gaspath multi-component degradation which often occurs in practice.

Methods of the group 2 (Fairbairn et al.; 1986; MacIsaac and Muir, 1991; Loboda, 2000). The total diagnosing process is divided into two steps. Primarily, to simplify the diagnosing the estimations of state parameters  are calculated by any identification procedure. Secondarily, a diagnosing decision is taken in the diagnostic space of state parameters: . This step is considerably simplified here because every state parameter indicates failure locality and development.

Advantages and disadvantages of the methods of each group depend on various factors (type of engine, life cycle stage, presence of prototypes, presence of accurate models etc.) and, generally, it is impossible to choose the more perspective method group. That is why trustworthiness indices were introduced and analyzed for both groups. For methods of the group 1 the indices are formed as average probabilities of correct/incorrect class recognition and for the group 2 these indices present the accuracy characteristics achieved on the gaspath parameters  and the state parameters  after the model identification.

The necessary software of the diagnostic models, identification procedures, and trustworthiness calculation algorithms was developed for the modern gas turbine power plant for natural gas pump units.

4. PROBABILISTIC INDICES OF TRUSTWORTHINESS

In the general form every class Dj is described in the region Wj* of the chosen diagnostic space  by the probability density function  of measured parameters. To determine the functions , the following assumptions were taken: 1) linear model adequacy, 2) uniform distribution  of the model values , 3) normal distribution  of the errors.

For the current measurement vector  the conditional posteriori probabilities , j=1-q  are calculated according to the Bayes formula:

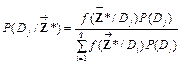,        (1)

where P(Dj) is a priory probability of the class Dj.

The set of the found probabilities , j=1-q, determines the trustworthiness of the diagnosing decision for one current measure only. Necessary characteristics of average trustworthiness, which are not connected with current measure, are calculated by means of statistical simulation of the measurements for every class, calculation of the probabilities (1), and their averaging.

The software RAPID (Loboda, 2001) was elaborated for computing such probabilistic indices. One variant of the indices is presented in the Table 1. The classification includes here the following component based classes: C – gas-generator compressor, CC – combustion chamber, T - gas-generator turbine, and PT – power turbine. Every element PDjl of the presented matrix signifies an average probability of the diagnosis Dj for measurements of the class Dl. The diagonal elements form the vector of correct diagnosis probabilities  y represent indices of distinguishing possibilities of gaspath classes, and parameter  formed as a mean number of these elements characterizes the total controllability of the engine with its measurement system.

A lot of calculations were fulfilled on the program RAPID to analyze numeric influence of factors that affect on the gas diagnosing trustworthiness. The list of these factors includes 1) measurement system structure, 2) measured parameters accuracy, 3) diagnosing regimes number and structure, 4) classification structure and type, 5) methodological errors, and any others.

The measured parameter faults were classified too and the measurement system controllability was estimated by the software RAPID. On base of the criterion  the analyzed power plant was also compared with engines of other types. The ways of measurement system optimization were established and practical recommendations to the power plant manufacturer were suggested.

However, the described approach that uses class description by the probability density functions  is not without its difficulties: simple type classes based on the linear model and ordinary theoretical parameter distributions may be realized only. That is why a new approach is developed.

Table 1. Probabilistic indices

Diagnosis probabilities PDjl
Diagno- sis Dj	Classes Dl
C          CC               T            PT
C          0.7597    0.0587       0.0940    0.0852
CC         0.0522    0.8241       0.0870    0.0195
T          0.0977    0.0973       0.8011    0.0135
PT         0.0904    0.0200       0.0179    0.8817
Correct diagnosis probabilities
0.7597     0.8241       0.8011    0.8817
Average probability  0.8167

5. PROBABILISTIC INDICES: NEW APPROACH

It is suggested describing the classes in the form of arrays of measured parameters (samples of measurement points) and applying the nonlinear model for failure development simulating. This approach to the trustworthiness problem permits forming the classes of any complex type including real classes constructed without model help. The computation algorithm incorporates the following items.

1) The trajectories of failure developments in the diagnostic space  are calculated for every class using the nonlinear model.

2) The reference samples  are formed by the calculation of the diagnostic parameters

             (2)

in Td points for every class Dj with usage of random number generators and the failure trajectories. In the Fig.1 four classes are shown as the samples . Class intersections and a requirement in recognition techniques can be noted.

3) The measurements

           (3)

of the testing samples  are generated by the same mode as in the item 2.

4) The criterion  is introduced of closeness of the current measurement point  and the failure class Dj presented by its reference sample. For every point of testing samples (3) and every reference sample  the criterion  is calculated and the nearest class is selected.

5) The trustworthiness indices PD, , and  mentioned above are formed by the averaging diagnostic decisions of the item 4.

Before the new approach practical usage, two tasks had to be solved: guaranteeing necessary accuracy of statistical simulation and selecting the best closeness criterion.

As a result of the calculations fulfilled it was established that the numbers Td=1000 and Tt=1000 of simulated points are sufficient and provide the necessary practical accuracy about 1% of the average probability . The needed computing time of about 40 min (Pentium IV, 1.7GHz) can be considered as acceptable.

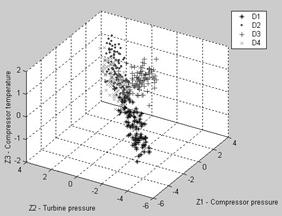
Fig.1. Reference samples

Five criteria  were chosen for a comparison:

- criterion 1 - mean inverse distance M(1/Rl) between a testing sample point and the reference points;

- criterion 2 - mean inverse quadratic distance M(1/Rl2) between a testing point and the reference points;

- criterion 3 - mean distance M(Rl) between a testing point and the reference points;

- criterion 4 - distance between a testing point and the class trajectory;

- criterion 5 - distance between a testing point and the gravity center of a reference sample.

The resulting indices  and  for the compared criteria are presented in the Table 2; the classification variant incorporates nine gas turbine classes (two classes for every already mentioned components and one more for the inlet device). It can be seen according to the index  that the criteria 3 and 5 provide the worst controllability. The criterion 4 looks as the best, but it is rather a theoretical criterion since in real class type the trajectory is not known. Change of the distance measure from 1/Rl (criterion 1) to 1/Rl2 (criterion 2) leads to better distinguishability of every class. Thus, the criterion 2 is selected as more perspective.

Table 2. Criteria comparison

Cri-teria	Correct diagnosis probabilities PTDj
D1    D2    D3      D4     D5     D6      D7     D8      D9
1      .654  .718  .765  .529  .739  .989  .755  .762  .746    .739
2      .740  .758  .792  .614  .788  .981  .788  .778  .778    .780
3      .543  .506  .711  .441  .644  .998  .708  .733  .684    .663
4      .891  .728  .896  .796  .889  .466  .869  .817  .839    .799
5      .643  .284  .757  .568  .656  .984  .732  .774  .558    .662

This approach related with class presentation by the reference samples promises interesting results. The model linearization effect and the influence of the diagnosing regime structure are investigated now. The next step will be to explore all possible remaining directions of diagnosing system optimization with model based and empiric classifications.

6. GROUP 1 ALGORITHM

With usage of the described probabilistic criteria, the algorithm on the base of Bayes formula was chosen and tuned up optimally for the real power plant diagnosing system. Special diagnostic testing of the power plant with physical modeling of four gaspath failures was organized to adjust finally the algorithm. Repeated testing had demonstrated the successful detecting all failures by the trained algorithm.

The Fig. 2 reflects the algorithm maintenance work. The complex index R of the compressor fouling probability and development is shown versus the power plant total work t;the compressor cleaning corresponds here to the point t = 7980. It can be concluded that the algorithm correctly reflects the fouling development and cleaning results.

7. GROUP 2: STATIC MODEL IDENTIFICATION

An identification algorithm is a principal part of any method of the group 2 and the identification procedure of the nonlinear static model was developed and verified on simulated and real data.

Any exact analytic solution for the identification estimations  does no exist due to model non-linearity, and numeric iteration procedure is applied.

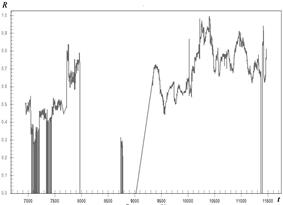
Fig.2. Fouling index

For the iteration n+1 the solution may be written as the sum

,                     (4)

where the current correction  presents a regularized solution of the linear system

 .             (5)

The generalized matrix  of this equation incorporates the influence matrices Hi calculated for N diagnosing regimes; the generalized vector  unites deviations  for the same regimes.

Two accuracy characteristics were introduced and analyzed during the procedure initial verification on model information: - average relative deviation of the model gaspath parameters from measured ones and  – average deviation of state parameter estimations from simulated values. It is necessary to note that dependency of the index  from main diagnosing factors presents a primary interest for detection algorithms and can be determined and studied by the failure simulating only because the true failure parameters are not known in real conditions.

During the verification, the failures were simulated by corresponding state parameter changes. The gaspath parameters were generated later by the model, random measurement noise was added, and the identification procedure was executed. This simulation and identification cycle was repeated numerously with independent variation of every sufficient factor affecting the identification process and statistical dependencies of accuracy parameters  and  from these factors were obtained. In general, an appropriateness of the identification procedure for diagnosing had been demonstrated, however a multi-regime configuration (N > 5-10) is required for necessary estimation accuracy.

8. IDENTIFICATION ON REAL DATA

Second stage of the identification procedure verification was fulfilled on maintenance data including the period of compressor fouling and next washing. The fouling presents the most common cause of engine performance deterioration and its influence on the gaspath parameters and on the state parameter estimations was a primary aim.

The data sample was formed from 1880 database registration points until and after the compressor washing and divided into the 47 consecutive portions of 40 points (regimes). During the calculations, the maintenance diagnosing process was imitated: the model identification was repeated for every portion and corresponding 47 consecutive estimations  were found.

The initial deviations dPc of compressor pressure measured values from the model ones, determined on the first identification step, are shown in the Fig.3, as well as the estimations of state parameters dGC and dEFFC which shift the compressor characteristic in the directions of the consumption and efficiency. Following conclusions may be drawn.

1) The random deviations in the compressor pressure plot are not so great and mainly do not exceed the level of 2%. Jump of the deviations dPc after the cleaning (point 918) and the total gas turbine degradation due to the fouling are well distinguished. Thus, the identified model satisfies the requirements to the norm function for gaspath monitoring.

2) The compressor characteristic shifts dGC and dEFFC correctly reflect the compressor clearing influence (after the portion number 23) and the following compressor state degradation, that is why the identification procedure suitability for fault detection algorithms is confirmed.

3) Accidental fluctuations in the estimations dGC and dEFFC related with the fluctuations in the deviations  are still significantly great and may mask fault effects. So, the next trustworthiness growth depends on the results of analyzing and elimination of the fluctuations in the deviations .

Great efforts were applied to study this problem. Table forms, graphic means for viewing and visualization of data, verifying calculations, and special instruments were used. As the result of these efforts, examples of model insufficient adequacy and cases of the power plant malfunctions such as measurement faults, abnormal functioning of variable inlet guide vanes, and anti-icing system defects were detected.

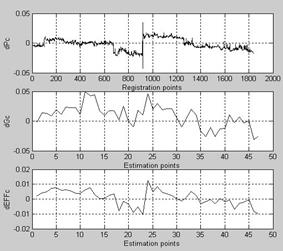
Fig.3. Identification results

As anyone can see from previous explications, a diagnostic application of static model identification requires a long-term period for initial data accumulation. It is also known that one transient process carries much more information about gas turbine state than one stationary regime therefore an accuracy of the identification estimations  could be sufficient for reliable diagnosing. That is why a dynamic model identification procedure has been proposed and analyzed for the short-term diagnosing.

9. DYNAMIC MODEL IDENTIFICATION

In the same manner as in the case of the static model identification procedure an identification procedure of the dynamic model was elaborated and tested on simulated data and real information. Although new algorithm is more critical to computer operating speed than the previous one, statistical measurement errors simulation and numerous repetitions of the identification are still possible.

The testing on simulated data has demonstrated a software correct functioning and a quick convergence of the iteration procedure (no more than 3-5 iterations are sufficient for estimation process stabilization). It was also demonstrated that the dynamic identification procedure ensures a stable detecting even 1 percent state parameter change on the background of the noise induced by real random errors of regular measured parameters. This conclusion is illustrated by the Fig.4 that contains simulated (thick line) and estimated (thin line) values of six state parameters: above mentioned compressor parameters, there are two corresponding parameters dGt and dEFFt for gas generator turbine and two parameters dGpt and dEFFpt for power turbine.

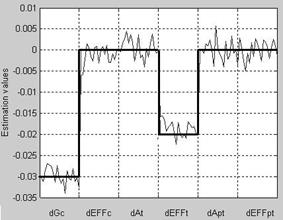
Fig.4. State parameter estimations

Maintenance parameter registration by the automatic control system of the power plant was used as a source of real information. Numerous cycles of the dynamic model identification and analysis of the results had confirmed an efficiency of the developed procedure. The nearest future task is to verify the procedure on the data including the results of physical failure simulation and/or real failure display.

10. CONCLUSION

Thus, three techniques are selected for including in the power plant automated diagnosing system: the algorithm based on the Bayes formula, the static model identification procedure, the dynamic model identification procedure. Adjustment and verification of these instruments have been fulfilled with usage of probability and accuracy criteria of diagnosing trustworthiness. It is recommended to include all three instruments in the diagnosing system because the advantages and disadvantages of these diagnosing techniques become apparent in different conditions. Applied originally for numerous calculations during trustworthiness problem investigations, described indices can be used again in maintenance conditions for a precise estimation of current diagnosing trustworthiness.