Statistical Testing Of Dynamic Model Identification Procedure For Gas Turbine Diagnosis.

1. Introduction

For a gas turbine that is considered as a complex and expensive system, condition monitoring technologies have the potential to save millions of dollars per year [1], through lowering fuel consumption, reducing catastrophic failures, decreasing mean time to repair, and optimizing maintenance planning. This will significantly reduce life cycle cost and improve competitive position of companies that maintain engines equipped with condition (health) monitoring systems.

Aircraft engine monitoring systems have become increasingly standard in the last two decades [2]. Above traditional aircraft application and usage in power plants of natural gas pumping and electrical power production, condition monitoring is used, for example, in shipboard [1] and battle tank [3] propulsion systems.

The thermodynamic (temperature, pressure, RPM, etc.) sensors are located at strategic points along the gas flow in the engine to provide more detailed thermodynamic picture of the engine’s state. The algorithms of failure detection that analyze registered thermodynamic parameters and use gas turbine models for diagnostic aims can be considered as principal algorithms of monitoring systems [2]. Gaspath failures can be detected by these algorithms, for example, compressor blade contamination, aerodynamic surfaces distortion, and seal wear as well as measurement system malfunctions.

Wide usage of mathematical models in diagnosing process is explained by high cost of physical failure modelling, an infrequent display of gas turbine failures, and other causes. Steady state regimes and corresponding static models are traditionally chosen for diagnostic needs; however transient regime analysis [4] is also involved in the diagnosis now.

Primarily, static thermodynamic models of different engines types and techniques of model identification were elaborated and applied in diagnostic aims [5]. A double effect was reached from this application: at first, higher model accuracy; at second, a diagnosing process simplification.

For feather diagnosing enhancement, a dynamic model and its identification procedure had been developed later and adapted to a stationary gas turbine power plant [6]. As every new tool perspective for practical implementation in active monitoring system, this procedure must be carefully verified. Therefore, a statistical testing of the dynamic model identification (DMI) procedure was carried out. The testing is described and the results are discussed in this paper as well as perspectives of DMI-procedure incorporating into the monitoring system.

2. Dynamic model identification

Dynamic nonlinear gaspath model describes behavior of thermodynamic parameters on transient regimes and can be presented by the common expression

,                    (1)

where the vector of regime and atmospheric conditions  is given as a function of time, and a separate influence of the time variable t is explained by an inertia nature of gas turbine dynamic processes. Every engine component (compressor, turbine, combustion chamber etc.) in this model is presented by its performance. The vector of state parameters  is used for describing and simulating the engine failures. These parameters are able to displace component performances in arbitrary directions and simulate different failures by this mode. The state parameters have a relative form; and the normal value is zero.

The thermodynamic parameters  of the model (1) are computed numerically as a solution of the system of differential equations in which the right parts are calculated from a system of algebraic equations reflecting the conditions of the components combined work on transient regimes. The measured values  differ from the model generated ones due to the model errors  and the measurement errors , therefore

.                   (2)

Similarly, the expression for regime and atmospheric conditions

                       (3)

is formed.

It is suggested to divide the total measurement error level into three components influencing on identification process in different ways: ε0Y, ε0U - levels of systematic errors; ε1Y, ε1U - levels of long-term random fluctuations that are changed from one transient regime to another; ε2Y, ε2U - levels of short-term random fluctuations that are changed during a transient regime.

The objective of model identification consists in finding such values of model internal parameters which minimize a discrepancy between model external parameters and measured ones. The state parameters  are chosen as such internal parameters that must be estimated. This is explained by the known fact that engine components theoretical performances used into the model are not sufficiently certain and may be specified on real data . So, the state parameter estimations  may be expressed as follows

.        (4)

Besides the better model accuracy resulting from such an adjustment, the simplification of the diagnosing process is reached because the found state parameters contain information of current technical condition of each component.

3. Identification procedure

Due to numeric nature of the dynamic model itself, any exact analytic solution (4) does no exist, and a numeric iteration procedure is applied. For any iteration of number n+1 the current estimation may be written as follows

,                       (5)

in which the current correction  presents a regularized solution of the linear system

,                   (6)

where C - matrix of influence coefficients of state parameters on thermodynamic parameters calculated in registration points 1, 2,…, NT of the transient regime chosen for the identification;  - vector of discrepancies between the model values  and measured ones  formed in NT corresponding time-points.

To solve the linear system (6), a standard technique is used that selects an optimal value of the regularization coefficient α. The variation boundary αmax may be changed. The iterations are repeated until a moment when current increments of state parameters and thermodynamic parameters will be sufficiently low or on reaching the established cycle number NI.

The software of the developed DMI-procedure includes about 70 program modules; around 90 percents of modules were imported from static model identification procedure and are time-proved. The software was tested on simulated data and real information and had demonstrated a correct functioning and quick convergence [6].

Although the DMI-procedure is critical to computer operating speed, a stochastic measurement simulation and numerous repetitions of the identification in the course of procedure statistical testing are still possible. In this paper, an influence of various factors on identification accuracy is investigated by such a testing.

4. Statistical testing description

The statistical testing was carried out in the following sequence: 1) the failures are simulated by state parameters  that displace component performances; 2) corresponding thermodynamic parameters are generated by the model with changed component performances; 3) a random measurement noise is added to these thermodynamic parameters and the inlet and control parameters; 4) the DMI-procedure is executed on the simulated data  and ; 5) error of the estimations  is determined.

In an external testing cycle this simulation and identification sequence is repeated NS times for reliable determination of obtained average accuracy. Behavior and accuracy of tested procedure are checked with the following cycle - averaged values (criteria):

dYi, dΘi - relative mean increments of thermodynamic and state parameters for every iteration i;

δY*i – mean discrepancies between model thermodynamic parameters and measured ones;

δΘi – mean discrepancies between simulated and estimated values of state parameters;

δΘj,  - discrepancies between simulated and estimated values of every state parameter ΘJ and on average.

The state parameters present a primary interest for detection algorithms therefore the criteria δΘj and  are chosen to define final identification accuracy. Other criteria are intended for the identification flow checking.

The factors affecting the behavior and accuracy and analyzed in the paper may be classified in the following way.

A. Internal parameters cyclic testing:

- cycle number NS.

B. DMI-procedure internal parameters:

- regularization coefficient boundary αmax;

- iteration number NI.

C. Identification conditions:

- measured thermodynamic parameters structure and number m;

- state parameters structure and number r;

- measurement error levels ε0Y, ε1Y, ε2Y, ε0U, ε1U, ε2U;

- dynamic process profile  given in NT points;

- simulated state parameters .

The number NS had been established first of all because it determines a total testing precision. Then with the known number NS, the proper values αmax and NI were estimated. After fixing the factors of the groups “A” and “B”, main part of the investigations was conducted: analyzing the group “C” factor, choosing optimal values, and forming the recommendations for diagnosis application.

Generally, there is not any information to consider above factors as independent and an idea to apply the complete factorial experiment to investigate the influence of the factors on the accuracy criteria looks as attractive. However, a great number of the factors, a sufficiently large required computer time (about 4 hours for a standard testing calculation on 1.7GHz Pentium IV computer), and impossibility to execute the DMI-procedure of the real engine at all theoretical points of such an experiment do not permit to realize this idea.

For this reason, other strategy had been chosen. A base calculation was established; factors were varied relatively the base calculation conditions and analyzed independently; most interesting and important results were verified by additional calculations in different conditions.

5. Testing results

5.1 Base calculation

The base calculation of identification procedure testing was executed in the following conditions:

1)  NS = 1000

2)  αmax = 5600, NI = 3

3)  m = 8 (all parameters of the power plant regular measurement system);

4)  r = 6 (a flow consumption parameter and an efficiency parameter for three components: compressor, high pressure turbine, free turbine);

5)  ε1Y = ε1U = 0.008 (this noise level ±0.8% corresponds to the regular measurement system; for the parameters of rotation speed the level is established 5 times lower), other noise components are equal to zero;

6)  vector  given in 5 time-points includes a linear change of high pressure rotor speed from 9450rpm to 10850 rpm during 2 seconds into the total interval of 4 seconds;

7)  Θmod1 = -0.03 (compressor flow parameter) and Θmod4= - 0.02 (high pressure turbine efficiency parameter); other 4 parameters are equal to zero.

A choice of noted values is explained in more details below.

Table 1 includes the base calculation results which show that first two parameters possess a lower accuracy and other ones have the approximately constant dispersion 0.0048. The accuracy mean number  = 0.00557 is used below for a comparison of calculations. The systematic error presented by the estimation displacements looks as insignificant.

Table 1

Identification accuracy of the base calculation

   δΘ1      δΘ2      δΘ3      δΘ4      δΘ5      δΘ6      

.00750 .00615  .00482  .00481  .00480  .00477  .00557

Averaged estimation displacements

.00132 -.00081 .00144  .00106  .00100 -.00066

It is practically interesting to know how clear is distinguished the simulated failure on the background of identification errors of such a level. To provide the answer, the basic calculation was repeated with an introduction of the failure simulation  after the testing cycle 200. The resulting estimations for four state parameters are plotted in Figure 1. It is evident from the plots Θ1 and Θ4 that the failure is statistically recognized.

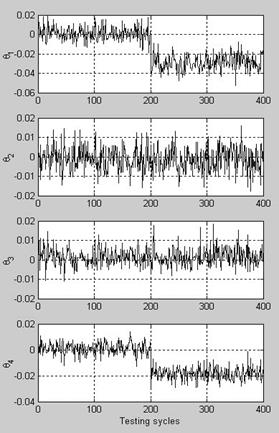
Fig.1. State parameter estimations

5.2 Testing precision

So, the first task of factors analysis was to establish proper cycle number NS to provide necessary precision level of the testing calculations. With the number 1000, the level [±(2-3)% for δΘj and ±1% for ] was reached. This level is sufficient for reliable determination of the factor influence on the criteria and presents a compromise between the achieved precision and required computer time.

5.3 Determination of identification

procedure parameters

To determine the identification procedure parameters, let analyze Figure 2 where identification flow in the base conditions (excepting NI = 10) is demonstrated. Common logarithms of current iteration increments dYi, dΘi and current accuracies δY*I, δΘi are plotted here versus iteration number variable. It may be noted that more and more short steps follow after the largest first one, and the increments are stabilized to the iterations 7-8, but accuracy stabilization is reached already on the iterations 2-3. Due to a flatness of the curves dY and dΘ in the right part of the plot, besides the increment limitation, an iteration number boundary was also introduced for loop termination and the value NI = 3 is accepted as basic.

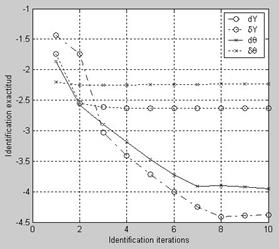
Fig.2. Identification process

Usually, the first iteration is carried out with small regularization coefficient and later it runs up to the maximum αmax therefore the limit αmax influences to identification behavior. However, the calculations with wide limit variation had been shown its weak influence on the accuracy and necessary iteration number. So, the values αmax = 5600 and NI = 3 were conserved.

5.4 Influence of structure of measured

and estimated parameters

In the investigations related with gas turbine model identification, the influence of measured and estimated parameters structure on identification accuracy is one of the traditional problems. Particularly, it is known that measured parameters number increase and/or estimated parameters number decrease lead to better estimation accuracy. This rule acts with one exception: all state parameters that really affect an engine state must be included in estimation least. In contrast, the accuracy will drop sufficiently.

To verify and specify the noted influence five calculations were fulfilled in addition to base calculation. Calculation conditions (differences from base calculation only) and mean accuracies are included in Table 2.

Consequent comparison of the calculations B1, A, and B2 as well as C1, C2, A, and C3 shows that the mentioned rule is kept generally. It may be noted too that the relation (m,r) is not linear and, besides the parameters number, the structure also influences on the accuracy.

So, for example, the weak influence of measurement system extension until 10 parameters (compare calculations A and B2) may be explained by the high self-descriptiveness of regular parameters and low one of additional parameters.

Other example: the enormous accuracy drop in the calculation C3. It is related with two states parameters included additionally for rotor inertia changes. Accuracy loss follows from a weak action of these parameters on the dynamic process in the calculation C3 conditions.

Table 2

Parameter number influence

Calculation designations

Calculation conditions

A

basic (m = 8, r = 6)

0.00557

B1

m = 6

0.01356

B2

m = 10

0.00554

C1

r = 2

0.00373

C2

r = 4

0.00484

C3

r = 8

2.05661

5.5 Influence of measurement error structure

During one transient regime, the long-term noise induces a constant displacement of all registered values of a thermodynamic parameter and may be considered as a systematic error which is transferred wholly on state parameter estimations. In contrast, the short short-term noise produces the random displacements and the averaged error only is transmitted on the estimations. So, it may be supposed beforehand that the short-term noise will induce lower identification error than the long-term one.

To verify this supposition, calculations with short-term noise simulation only were executed and the results are presented in Table 3 as well as the base calculation result. From comparison of the calculations D1 and C follows that the short-term noise causes more than two times lower estimation error. Comparison of the calculations D1, D2, and D3 confirms noted in the part 5.4 influence of the measured parameters number m.

Table 3

Short-term noise calculations

Calculation designations

Calculation conditions

A

basic (ε1Y=ε1U=0.008)

0.00557

D1

ε2Y=ε2U=0.008

0.00256

D2

ε2Y=ε2U=0.008, m = 6

0.00835

D3

ε2Y=ε2U=0.008, m=10

0.00254

In constant identification conditions, systematic measurement errors will induce identification systematic errors. On the other hand, the condition change may lead to a shift of the estimation and estimation errors.

To evaluate this effect, three sets of fixed systematic measurement errors were formed and DMI-procedure was repeated for every set in the seven different condition variants. Related with variant change scatters of six estimated parameters are presented in Table 4. It is seen that the scatters may reach the level of simulated state parameters. So, systematic measurement errors may induce the random estimation errors when random changes of identification conditions take place. Systematic estimation errors are not considered here because it is supposed that in the diagnosis, the time-series of estimation will be analyzed and a relative estimative change only will be considerable.

Table 4

Systematic measurement error influence

Sets                    Estimation scatters

1        0.0363  0.0139  0.0170  0.0076  0.0262  0.0146

2        0.0099  0.0010  0.0059  0.0035  0.0074  0.0032

3        0.0122  0.0064  0.0121  0.0047  0.0143  0.0072

5.6 Influence of dynamic process profile

 and failure type

To estimate dynamic process and failure type on the identification accuracy, the process profile (regime parameter change during the process and process total time) and failure development were modified. The results presented in Table 5 display the estimation error stability to these factors (the scatter does not exceed the testing error level).

So, an attempt had been made to analyze systematically a maximal number of factors affecting the identification accuracy and to determine numerically this influence. Applied statistical testing included the model-based simulation of failures and generation of random measurement errors with theoretical distribution.

Table 5

Calculations with variation

of dynamic process profile and failure type

Calculation designations

Calculation conditions

A

basic

0.00557

E1

3 times decrease of regime parameter change

0.00580

E2

5 times increase of time interval

0.00561

F1

3 times decrease of failure development

0.00557

F2

absence of failure

0.00555

However, it is clear that conducted investigations do not resolve all difficulties of such a challenge as gas turbine dynamic model identification. Besides the known problems of static model identification [7] that are actual here too, new ones, for example, a dynamic measurement error problem, are expected. Not all of these problems may be resolved by means of the model-based simulation and one of the near future tasks will be to verify the procedure on the data of physical failure simulation and/or real failure display.

6. Conclusion

Thus, to verify the developed dynamic model identification procedure for including into gas turbine health monitoring systems, the statistical testing had been carried out. A lot of factors affecting the identification accuracy were analyzed. Sufficient factors had been determined, for instance, the systematic and random long-term measurement errors. An invariance of the accuracy to other group of factors such as dynamic process profile and simulated failure type was also noted.

The achieved accuracy level is sufficient to suggest this identification procedure for realization in monitoring systems. The procedure promises to make gas turbine diagnosing more universal by enabling attraction of transient regimes.