Identification Procedure Development of Gas Turbine Nonlinear Dynamic Model.
1 Introduction
Modern gas turbine power plants represent powerful and efficient sources of mechanical energy for numerous industry branches and transport objects. Maintenance cost reducing of these complex technique objects, as well as a rise of their reliability and safety characteristics considerably depend on a perfection of applied Automatic Control Systems and Automated Diagnosing Systems.
Design of gas turbine itself and its systems is deeply related with calculations on the base of gaspath mathematical models of different complexity, and the identification procedure represents not only an effective instrument to raise an accuracy of the models and related calculations but also an important component of diagnosing and control algorithms. Industrial application such instruments as nonlinear mathematical model and its identification procedure becomes a common practice [1, 2].
Last computer progress stimulates an elaboration and application of sophisticated elements of control and diagnosing systems, such as nonlinear dynamic model identification procedure considered in this paper.
2 Gaspath Mathematical Models
Numerous gas turbine gaspath models practically used for the control and diagnosing may be classified as follows: a) linear and nonlinear; b) static and dynamic; c) according to a depth of description.
Two types of the models are principle and most complex: nonlinear static model and nonlinear dynamic model. Other types may be generated by means of these ones.
The first type is multi-regime gaspath model, in which every component (compressor, turbine, combustion chamber etc.) is presented by its performance. In a common form this model is described by the dependency
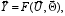(1)
where
the vector
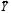of
gaspath parameters (measured and inaccessible for the measurement)
depends on the vector
of gas
turbine regime parameters (including atmospheric condition parameters
too) and the vector
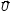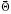of
gaspath state parameters.
In capacity of state parameters the parameters of gas turbine component performance (performance parameters) are chosen. These parameters are able to move and deform the component performances and, as a result, to adjust the model performance to the real one or simulate engine failures.
Mathematically, the relation (1) is found as a solution of the system of algebraic equations reflecting the conditions of the components combined work on steady-state regimes.
A modification of these combined work equations to the conditions of transient regimes permits to form a dynamic model (second type model) of the following view:
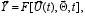(2)
where
the vector of regime parameters, in contrast to the static model, is
given as a function of time
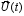, and a
separate influence of the time variable t
is explained by an inertia nature of gas turbine dynamic processes.
In the model (2) an influence of main inertia factors, the inertia moments JGG and JFT of gas-generator and free turbine rotors correspondingly, is taken into account, and differential movement equations realized in the model are as follows:
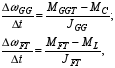(3)
where
-
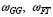rotation speeds of gas generator and free turbine;
-
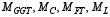acting moments of gas-generator turbine, compressor, free turbine,
and external load applied to the free turbine.
In
addition to the performance parameters, the special parameters ΔJGG
and ΔJFT
were introduced in the vector
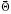for
correcting the initial inertia moments in identification aims.
Numerous developments of static and dynamic models of pointed types and static model identification researches were fulfilled using the universal gas turbine model approach [3-6]. These developments were applied to the gas turbines of basic schemes, and the procedure of dynamic model identification, which is described below, was elaborated later on a base of this previous experience. The procedure was adapted to the real gas turbine used as a drive of natural gas centrifugal compressor.
3 Identification Procedure of Nonlinear Dynamic Model
The
real measured data
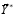differs
from the model data
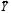due to
the model and measurement errors, and an object of dynamic model
identification is to find such state parameter estimations
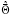which
minimize the error level. Therefore, a task of dynamic model
identification may be classified as optimization problem, and the
estimations may be found according to the following expression
written in common form
.
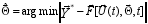(4)
Due
to model non-linearity any exact analytic solution for the
estimations
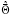does no
exist, and the following numeric iteration procedure is applied.
For any iteration of number n+1 the solution may be written as follows
,
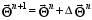(5)
where the current
correction
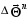presents the regularized solution
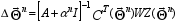(6)
of the linear system
,
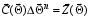(7)
where
-
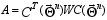Fisher information matrix; W
– weight matrix; I
– single matrix;
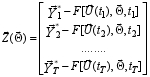- generalized vector
of deviations of the model values from measured ones formed in T
calculation points of a transient process interval selected for the
identification;
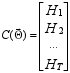- generalized matrix
of influence coefficients;
H1,
H2,
… , HT
– partial matrixes of influence coefficients of state parameters
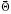on
gaspath measured parameters
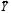calculated in correspondent points 1,
2,…, T.
The iterations are repeated until a moment when current corrections of state parameters and gaspath parameters will be sufficiently low.
During
the iteration calculations according to described above scheme,
dynamic model is called numerously: one time to calculate the vector
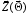and r+1
times for determination of the matrix
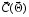, where
r
is a size of the vector
.
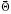4 Software Structure
Developed software of the nonlinear dynamic model identification presents a complex program package and approximately consists of 70 program modules. Block-scheme of the program package (see Figure 1) includes 10 module of high level. Other modules, directly related with gas turbine components calculations, are united in the lowest block.
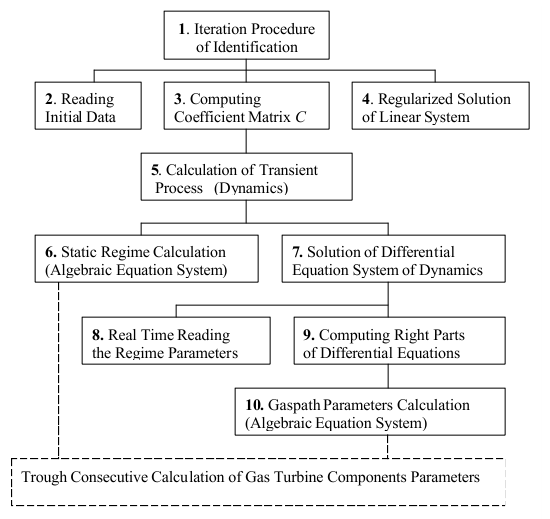
5 Testing the Software
The testing was separated on two stages: a) on simulated data; b) on real data. Two objects are pursued: at first, to check the identification procedure functioning; at second, to estimate the possibility of the procedure application in gas turbine control and diagnosing systems. Characteristics of identification quality, which is connected with the accuracy achieved on gas path parameters and state parameters, were chosen as criteria.
Testing on simulated data has demonstrated the software correct functioning and a quick convergence of the iteration procedure.
Maintenance
parameter registration by the gas turbine automatic control system
was used as a source of real information. The following parameter
structure was selected: temperature tН
and pressure PН
of atmospheric air, fuel consumption Gf
and power turbine rotation speed nPT
(vector
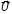); 7
regular measured parameters (vector
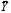); 6
estimated parameters of gas turbine component performance: two fault
indices (a gas consumption parameter and an efficiency parameter) for
every of principle mechanic components: axial compressor, gas
generator turbine, free turbine (vector
).
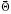Numerous cycles of dynamic model identification on the real information has confirmed the correct functioning and quick convergence.
6 Conclusion
Described in this paper the development and testing of the identification procedure of gas turbine nonlinear dynamic model may be considered as a first phase of total research work in this direction. The investigations are continued to determine the best way of this instrument practical application for control and diagnosing systems.
7 References
G.W. Fairbairn, J.R. Nisbet, I.C. Robertson. Performance testing and monitoring of compressor units/ 52nd Autumn Meeting of the Institution of Gas Engineers (The Queen Elizabeth II Conference Center, November 11-12, 1986). Communication N 1306, 32p. ISSN 0367-7850.
Bernard D. MacIsaac, David F. Muir. Lessons learned in gas turbine performance analysis/ Canadian Gas Association Symposium on Industrial Application of Gas Turbines (Banff, Alberta, October 16-18, 1991), 28p.
Loboda I.I. Optimization of the procedure of identification of a gas turbine nonlinear mathematical model / Progress. Process Engineering. Quality: Transactions of the Second Congress of the Ukrainian Engine Designers with Foreign Involvement (September 22-25, 1997). -Kiev-Kharkov-Ribachye, Ukraine, 1997. -pp.94-100 (in Russian).
Loboda I.I., Dema T.F. Development of dynamic module model of turbofan engine with ideal control system / Aerospace Technics and Technology. Journal: Kharkov Aviation Institute, Kharkov, Ukraine, 1999- Issue 9, pp.85-89 (in Russian).
I.I. Loboda. Results of identifications of gas pump unit nonlinear mathematical model with maintenance data/ Aerospace Technics and Technology. Journal: Kharkov Aviation Institute, Kharkov, Ukraine, 2000- Issue 19, pp. 385-392, (in Russian).
I. Loboda, E.L. Santiago. Problems of gas turbine diagnostic model identification on maintenance data / CD-ROM: Memorias del 6 Congreso Nacional de Ingeniería Electromecánica, ESIME-Zacatenco, Mexico, 27-30 noviembre 2001, pp.332-334.