Algorithm Of Optimal Load Distribution Between Gas Pump Units Of Compressor Shop.

The function of a compressor shop is to restore the gas pressure reduction caused by frictional pressure losses in a pipeline. Shop compressors are driven by gas turbines which all together are known as gas pump units. Gas turbines use natural gas as fuel and minimizing this fuel usage is a major objective in the control of the compressor shop.

That is why it is important to choose the structure of functioning units and their loads (individual pumped gas consumptions) to provide maximal gas saving. This task is too complicated for a shop personnel and is needed to be automatized.

This paper describes the algorithm of load distribution between units of compressor shop according to the condition of minimal total consumption of fuel gas.

-  .- necessary total volume consumption of the gas pumped by the shop (the consumption is corrected to the normal atmospheric conditions);

-  N–  total number of shop units;

-  - functional dependencies of unit mass fuel consumption Gf.i from corrected volume consumption Qn.i pumped by the unit;

-  - low unit consumption limit depending on compressor surge line position and idle regime power of gas turbine;

-  - high unit consumption limit connected with gas turbine power and rotation speed limitations.

Mentioned task of fuel saving is a typical problem of the optimization with limitations:

,

, .      (1)

It is convenient for solving of the problem to divide the units into two group in following manner. The first group includes the units with fixed pumped gas consumption. Three types of the fixation are distinguished:

1)  the unit is shut down ( ), 2) the unit works on the low limit ( ), 3) the unit works on the high limit ( ).

Other units of float consumption parameters are collected in the second group.

The problem is solved by means of analyzing all possible variants of the first group structure, searching the minimal fuel consumption of the second group units for every such variant, calculating the total fuel consumption of the shop which is taken as a local optimum, and defining a global optimum by means of local optimum comparison.

The calculations are carried out in a following sequence:

1.  It is supposed initially that all units are concentrated in the second group. For these units the best decision is looked for and taken as a current value of the global optimum parameter GfΣopt.

2.  It is supposed later that a part of the units belongs to the first group and the number m of these units is set in a cycle from 1 to N-1.

3.  For every value of parameter m, m inserted cycles of first group structure changing and the cycle of consumption fixation type changing are organized.

4.  For every generated in item 3 variant (variant of first group structure and consumption fixation type) the optimal loads  of N-m units of the second group is searched and the local minimum of total consumption GfΣ is calculated.

5.  If the found consumptions  (see item 4) lie between the limits then the correspondent value GfΣ is compared with the parameter GfΣopt. If the first is lower the parameter GfΣopt is refreshed and the variant of consumptions  is recorded ( = ).

The calculations described in items 4 and 5 are repeated numerously inside of external (item 2) and internal (item 3) cycles. Thus, parameter GfΣopt will rich global optimum value after completing the cycles.

It is necessary to describe in details the procedure of local minimum searching mentioned in item 4.

New variables are introduced:

 - total consumption of a pumped gas for n=N-m optimized units;

xi = Qn.i , i=1, n-1 consumption variables for n-1 units.

The consumption of the unit number n is expressed as

 .

After this variable introduction the expression for total fuel consumption G*fS for n units will look as follows:

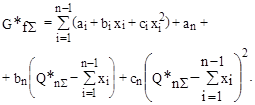  (2)

The condition of the expression (2) minimum (particular derivatives are equal zero) leads to the system of n-1 linear equations:

,  i=1,...,n-1.             (3)

Due to simplicity of this system the solution is obtained without the application of matrix conversion.

After subtracting the equation number j of the system (3) from the equation number i the dependency between any two variables xi and xj is derived:

 .                           (4)

Then it is necessary to change all variables xj, j=1, n, j¹i by the expressions (4) in the equation number i of the system (3) and after a few of conversations the solution is derived:

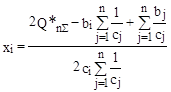 .                  (5)

The algorithm is tested on data obtained from the diagnostic model of real gas pump unit. This model has an ability to simulate the deterioration of unit components. It permits to check algorithm functioning in the conditions of different technical state of shop units.

The result of fulfilled numerous calculations have lead to following conclusions.

1.  The algorithm always leaves the minimal number of the operating units which are necessary to pump the total consumption . This tendency is explained by a considerable growth of gas turbine specific fuel consumption on the low regimes. Clear that only most efficient units are chosen and they operate near their high limits.

2.  If for pumping of total gas consumption the deteriorated unit is included in the list of operating units then the individual load of this unit has not be obviously minimal. In this case not absolute fuel consumption level is significant but a value of pumped gas consumption derivative from fuel consumption.

3.  Difference in total fuel consumption between the variant of optimal load distribution and, for example, the variant of equal load distribution lies on the level of a few percents. That is why the algorithm efficiency in great scale depends on initial data accuracy. Necessary accuracy may be obtained in the conditions of automatic diagnosing system only, when algorithm initial data are regular refreshed with taking into account the current unit technical state and current parameters of pumped gas.

4.  Since the algorithm application leads to the high operational regimes and it is famous that fast turbine life usage takes place on these regimes, the further algorithm development is connected with taking into account the turbine life usage for the optimum criterion formation.