Loboda Igor

Radial Basis Functions For Gas Turbine Fault Recognition

Introduction

I.І. Loboda, L.A. Miro Zarate, A.E. Leal Bolanos АВИАЦИОННО-КОСМИЧЕСКАЯ ТЕХНИКА И ТЕХНОЛОГИЯ, 2010, № 10 (77)

In order to improve gas turbine reliability and reduce maintenance costs, many advanced condition monitoring and diagnosis systems have been developed recent decades. A diagnostic process in such a system can be divided in some stages such as feature extraction from raw input data, fault detection, fault identification, and prognosis. Final efficiency of diagnostic decisions will depend on quality of each stage.

In the monitoring system, fault identification algorithms based on the gas path analysis may be considered as important and sophisticated. These algorithms also use pattern recognition techniques, mostly different artificial neural networks [1 – 3].

Among the networks applied, a multilayer perceptron has emerged as the most widely used in gas turbine diagnostics [3]. Our study [4] also shows that the perceptron’s fault recognition is accurate enough. However, other network types begin to compete with the multilayer perceptron, in particular, a network with radial basis functions or radial basis network (RBN) [5].

In the present paper, the application of the RBNs to gas turbine fault recognition is examined. To better assess efficiency of this network, it is compared with the perceptron and the focus is on recognition accuracy. Comparative calculations were carried out in MATLAB®. A gas turbine driver for a pipeline gas pumping unit has been chosen as a test case to perform the comparison. A mathematical model of this engine is employed for fault simulating. In order to generalize the conclusions on the network efficiency, compared techniques are verified under different engine operation and diagnosis conditions.

1. Approach used

In the present paper the faults of the chosen engine are simulated mathematically because of rare appearance of real faults and high costs of physical fault simulation. The model  of the gas turbine driver computes the monitored gas path variables  as a function of a vector of control variables and ambient conditions  and a vector of fault parameters . The model is called a thermodynamic model and can be classified as static, non-linear, and one-dimensional. The vector  feeds the engine stationary operating conditions into the model. While the vector  helps to take into account an actual engine health condition. The nominal values of correction factors  correspond to an engine baseline. Changes  entered into the model provide some shifting of the engine component performances in given directions and the corresponding deviations of monitored variables, thus simulating different faults of variable severity.

In the process of fault simulation, deviations  for each monitored variable  are generated. Every deviation is composed of two components: a systematic component  and a random component , i.e. . The systematic component is induced by the faults implanted in the model, while the component  takes into account possible errors in the deviations. The deviation  is normalized so that the random variable  is limited by the bounds "-1" and "1" for all monitored variables. The deviations of these variables form a vector , which is a pattern to be recognized when the diagnosis is performed. A lot of patterns  are generated to build the classification described below.

Existent variety of gradual degradation mechanisms and abrupt faults is too great to distinguish all of them. Furthermore, maintenance personnel do not need such a detailed diagnosis. That is why, the faults should be united into a limited number of classes. The used fault classification is formed on the hypothesis that an actual engine condition pertains to only one of preset q classes . In the space of normalized deviations , each fault class is represented statistically by its own sample of patterns generated by the model. In order to reach satisfactory numerical accuracy, a sample of the class usually comprises 700 patterns or more. During the pattern generation, a fault severity is given by the uniform distribution of the fault parameter changes  within the interval (0, - 5%) while the errors  are generated according to the Gaussian distribution. Two types of fault classes are simulated. A single fault class is formed by changes of only one fault parameter and a multiple fault class implies independent variation of two parameters of the same engine component. From classes of each type, a separate classification is composed.

A nomenclature of possible diagnosis  corresponds with the accepted classification . To make a diagnosis d, the chosen network, perceptron or RBN, computes a closeness measure between a current deviation vector  (pattern) and each item Dj of the classification. The closest class is recognized as a current diagnosis. Before making diagnostic decisions, the network is trained on the fault classification patterns. That’s why a totality of classification patterns is called a training set.

The multilayer perceptron is a feed forward network trained with the back propagation algorithm. Perceptron foundations can be found in any textbook on neural networks or in Matlab Help [7] and only a perceptron structure is described below. The used network presented in Fig.1 has one hidden layer and sigmoid activation functions. The number of the network inputs is equal to a number m of monitored variables (dimensionality of the patterns ). The quantity of the outputs equals to a number q of analyzed classes. Each output gives a closeness measure between an actual input pattern  and the corresponding class; the maximal output indicates a current diagnosis. The optimal hidden layer’s size of 12 and the best training algorithm, resilient backpropagation, were determined previously in [6].

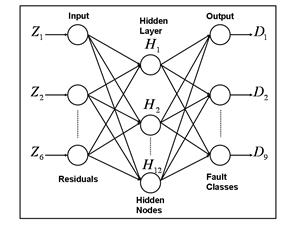
Fig. 1. Perceptron structure

The other analyzed technique, radial basis network, may require more neurons than the perceptron; however it can often be trained within the same time that is necessary for the perceptron. It is a favourable factor that the training set comprises thousands of patterns because the RBFs work better when many training patterns are available [7]. Note that a RBF’s neuron differs from a perceptron neuron. Here the input n to a radial basis transfer function is a vector distance between a weight vector  and an input vector , multiplied by a bias b i.e. . A neuron output computed by the transfer function is . The function has a maximum of 1 when the distance is 0. The output decreases when the distance between  and  increases. The bias b allows adjusting the neuron sensitivity.

Figure 2 helps to illustrate RBFs’ operation. The presented radial basis network includes two layers: a hidden radial basis layer (S1 nodes) and an output linear layer (S2 nodes). The input vector  and an input weight matrix IW1,1 produce a distance vector having S1 elements. The bias vector b1 scales these distances and a MATLAB transfer function radbas converts the scaled distances into an output vector  of the hidden layer. The output layer operates like a usual perceptron output layer and produces an output vector  of S2 elements.

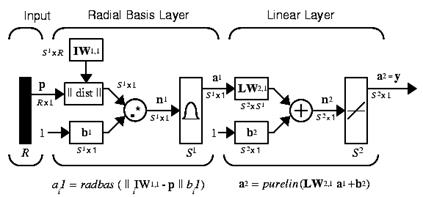
Fig. 2. Structure of the radial basis network

Although the networks, perceptron and RBN, adjusted to the data of the training set, are ready for gas turbine fault recognition, they must undergo statistical testing. To that end an additional set − called a validation set − is formed just like the training set. The only distinction is that different seeds are used to initialize the random number generators. During the testing, every pattern of the validation set enters into the network and the latter makes the corresponding diagnosis. As the pattern’ class is known beforehand, it can be compared with the diagnosis and we can ascertain whether the diagnosis was correct. That is why for each class , a probability  of a correct diagnosis can be calculated. It determines the distinguishability of this class against the background of the other classes. The probabilities calculated for all classes make up a vector . Mean value of these probabilities denoted as  allows determining the total engine’s diagnosability and is employed as a criterion for tuning and comparison of the employed networks.

In order to compare two chosen networks, they were embedded into a special testing procedure designed in MATLAB. In this procedure the both networks have the same input data, namely, training and validation sets. Output data, mean probabilities  and  of a correct diagnosis, are computed for the training and validation sets correspondingly. Quantity  is a principal criterion to choose the best network, while quantity  helps to control so-called network overtraining. Although in every comparative calculation, input data for the perceptron and RBN are the same, the calculations with the testing procedure are repeated for different comparison conditions (network parameters, diagnostic conditions, and engine operating conditions). This is necessary to draw sound conclusions on efficiency of the compared techniques. These varying conditions are described in the next section.

2. Comparison conditions

All calculations are executed with constant structure and accuracy of measured gas path variables, which correspond to a gas turbine regular measurement system. The other computational conditions described below are varying.

A. Seed number. The comparative calculations are repeated for two different seeds in order to exclude the influence of a particular distribution of random numbers.

B. Number of nodes in the hidden layer. The above calculations are repeated for two different numbers of nodes in the hidden layer because it is difficult to determine an exact node number.

C. Classification parameters. Two classification variations are considered. The first incorporates nine single classes. The second includes four multiple classes corresponding to the principle modules (compressor, combustion chamber, compressor turbine, free turbine). It is not known beforehand which classification variation will be more adequate in real conditions. That is why, the previously described calculations are performed for the both variations.

D. Gas turbine operational conditions: Two gas turbine operating points are analyzed. They are close to engine maximal and idle regimes and are set by different high pressure rotor speeds under standard ambient conditions. All the above calculations are carried out for each operating point.

As can be seen, four factors are varied independently and each factor has two values. Consequently, a total number of comparative calculations equals 16. The following section describes their results.

3. Comparison results

Before performing principal calculations described above, some preliminary studies have been performed. As a result, optimal parameters of the fault classifications and networks have been found. In particular, the numbers of 700 simulated patterns for each single fault class and 1000 patterns for each multiple fault class were established. Basic and enlarged numbers of hidden layer nodes were chosen as well: 12 and 24 for the perceptron, and 27 and 90 for the RBN.

Table 1, which contains results of some principal calculations, helps to estimate quality of the network training process, namely the absence of the over training effect. It can be seen that this effect does not take place in the presented calculations because the differences are small between the probabilities  and  as well as between the basic and early stopping options.

Probabilities of a correct diagnosis  computed for the validation sets are given in Table 2 for all principal calculations. As can be seen, for the enlarged node numbers the RBN demonstrates slight enhancement of diagnosis accuracy compared with the perceptron (0.3-0.5 per cent increment of ).

Table 1

Results of training process verification (computation conditions: regime 1, seed 1, singular class type)

Network type	Probability	Basic node number	Enlarged node number
Basic option	Early Stopping option	Basic option	Early Stopping option
Perceptron		0,8133 0,8129	0,8108 0,8103	0,8160 0,8135	0,8165 0,8168
RBN		0,8070 0,8110	N/A	0,8190 0,8167	N/A

Table 2

Network comparison results (probabilities  obtained on the validation set)

Class type	Seed	Network type	Regime 1	Regime 2
Basic node number	Enlarged node number	Basic node number	Enlarged node number
Singular	1	Perceptron	0,8129 0,8110	0,8135 0,8167	0,8025 0,7986	0,8027 0,8078
Base radial
2	Perceptron	0,8127 0,8090	0,8151 0,8160	0,8003 0,7970	0,8005 0,8000
Base radial
Multiple	1	Perceptron	0,8755 0,8733	0,8760 0,8805	0,8665 0,8662	0,8650 0,8700
Base radial
2	Perceptron	0,8738 0,8740	0,8733 0,8780	0,8635 0,8685	0,8670 0,8702
Base radial

Conclusions

Thus, the comparison of two recognition techniques, multilayer perceptron and radial basis network (RBN), has been performed in the present paper. The necessary fault classification was formed with the use of the thermodynamic model of a gas turbine for driving centrifugal compressors in natural gas pipelines. The classification and the recognition techniques were embedded into a special testing procedure that computes for each technique the probabilities of a correct diagnosis. In order to draw sound conclusions about the compared techniques, the comparative calculations were executed by means of
the mentioned procedure for different network parameters, diagnostic conditions, and engine operating conditions.

Summing up the comparison results, it can be stated that the application of the RBN yields some enhancement of gas turbine diagnosis reliability. However, a greater complexity of the RNFs should be taken into account when a recognition technique is chosen for a real gas turbine monitoring system. This paper is only the first comparative study of the perceptron and RBN. The investigations will be continued to draw the final conclusion on the applicability of these recognition techniques in gas turbine diagnostics.

Acknowledgments

The work has been carried out with the support of the National Polytechnic Institute of Mexico (research project 20101199).

References

1 Roemer M.J. Advanced diagnostics and prognostics for gas turbine engine risk assessment /
M.J. Roemer, G.J. Kacprzynski. − Proc. ASME Turbo Expo 2000, Munich, Germany, 2000. − 10 p.

2 Ogaji S.O.T.Gas path fault diagnosis of a turbo­fan engine from transient data using artificial neural networks / S.O.T. Ogaji, Y.G. Li, S.Sampath, et al.− Proc. ASME Turbo Expo 2003, Atlanta, Georgia, USA, 2003. − 10p.

3 Volponi A.J. The use of Kalman filter and neural network methodologies in gas turbine performance diag­nostics: a comparative study / A.J. Volponi, H. DePold,
R. Ganguli // Journal of Engineering for Gas Turbines and Power. −2003. − Vol. 125, Is. 4. −Р. 917-924.

4 Loboda I. Gas Turbine Fault Recognition Trustworthiness / I. Loboda, S. Yepifanov // Cientifica. Revista de la ESIME-IPN, Mexico. − 2006. − Vol. 10, Num. 2. − Р. 65-74.

5 Shankar P. A neural network based adaptive observer for turbine engine parameter estimation / P. Shankar, R.K. Yedavalli.− Proc. ASME Turbo Expo 2006, Barcelona, Spain, 2006.− 9p.

6. Loboda I. Gas turbine fault recognition by artificial neural networks / I. Loboda, M. Nakano Miya­take, A. Goryachiy, E.M Gutiérrez Mojica, J.E. González Aguilar.− Memorias del 4to Congreso Internacional de Ingenieria Electromecanica y de Sistemas, ESIME-IPN, Distrito Federal, Mexico, 2005. − 6p.

7. MATLAB manual. Neural Network Toolbox.

Поступила в редакцию 3.06.2010

Рецензент: канд. техн. наук, профессор кафедры конструкции авиадвигателей Ю.А. Гусев, Национальный аэрокосмический университет им. Н.Е. Жуковского «Харьковский авиационный институт», Харьков.

РАДІАЛЬНІ БАЗИСНІ ФУНКЦІЇ ДЛЯ РОЗПІЗНАВАННЯ ДЕФЕКТІВ ГТД

І.І. Лобода, Л.А. Мiро Сарате, А.Е. Леаль Боланьос

Штучні нейронні мережі являють собою розрахунковий метод що швидко розвивається у багатьох областях застосування, включаючи діагностику ГТД. Ця стаття досліджує мережу, засновану на радіальних базисних функціях (радіальна базисна мережа) і застосовується для розпізнавання дефектів проточної частини. Для того, щоб оцінити ефективність радіальної базисної мережі (РБМ), вона порівнюється з багатошаровим персептроном. З метою коректного порівняння вхідні дані в кожному порівняльному розрахунку однакові для обох мереж. Порівняльні розрахунки повторюються для різних варіантів цих даних, що дозволяє одержати більш загальні висновки по застосовності РБМ. До цілей роботи відноситься підгонка мереж, їх порівняння та оцінка ефективності РБМ на основі критерію ймовірності правильного розпізнавання дефектів. Результати порівняння показують, що РБМ є перспективним засобом для діагностування ГТД.

Ключові слова: ГТД, діагностика проточної частини, радіальна базисна мережа, ймовірность правильного розпізнавання дефектів.

РАДИАЛЬНЫЕ БАЗИСНЫЕ ФУНКЦИИ ДЛЯ РАСПОЗНАВАНИЯ ДЕФЕКТОВ ГТД

И.И. Лобода, Л.А. Миро Саратэ, А.Э. Леаль Боланьос

Искусственные нейронные сети представляют собой быстроразвивающийся расчетный метод для многих областей применения, включая диагностику ГТД. Данная статья исследует сеть, основанную на радиальных базисных функциях (радиальная базисная сеть) и применяемую для распознавания дефектов проточной части. Для того, чтобы оценить эффективность радиальной базисной сети (РБС), она сравнивается с многослойным персептроном. С целью корректного сравнения входные данные в каждом сравнительном расчете одинаковы для обеих сетей. Расчеты повторяются для различных вариантов этих данных, что позволяет получить более общие выводы по применимости РБС. К целями работы относится подгонка сетей, их сравнение и оценка эффективности исследуемой нейронной сети на основе критерия вероятности правильного распознавания дефектов. Результаты сравнения показывают, что РБС является перспективным средством для диагностирования ГТД.

Ключевые слова: ГТД, диагностика проточной части, радиальная базисная сеть, вероятность правильного распознавания дефектов.

Лобода Игорь Игоревич – канд. техн. наук, доцент, доцент Национального политехнического института, Мехико, Мексика, e-mail: loboda@calmecac.esimecu.ipn.mx.

Миро Сарате Луис Анхель – студент магистратуры Национального политехнического института, Мехико, Мексика.

Леаль Боланьос Адриан Энрикэ – студент магистратуры Национального политехнического института, Мехико, Мексика.