Probabilistic Neural Networks For Gas Turbine Fault Recognition
The main focus of this paper is reliable fault recognition for gas turbines. Gas path models are employed to describe different faults of variable severity. To recognize them, two methods are used and examined in the paper. The first method is based on the Bayesian recognition while the second applies neural networks. The recognition process for the both methods is simulated numerously under the conditions of random measurement errors, and diagnosis errors are fixed. The objectives are to verify the methods statistically, adjust them, and compare the networks' recognition errors with the Bayesian recognition ones. To make the accuracy analysis more general, the paper compares the methods for two fault classification variants and different gas turbine operating conditions.
Gas turbine model, neural networks, statistical verification of diagnostic methods, fault recognition accuracy
1. Introduction
High availability and limiting degradation are very important for the new generation of high temperature and high output gas turbines. Advanced condition monitoring systems for turbomachines have been designed and maintained over the recent decades. These systems include gas path analysis techniques to compute and correlate all performance variables of the engine gas path and, in so doing, relate fault parameters to measured variables.
Although faults affect measured and registered gas path variables (pressures, temperatures, rotation speeds, and so on), the impact of changes in operational conditions is much stronger. So, fault effects remain latent. That is why in diagnostic algorithms, raw measurement data should be subjected to a complex mathematical treatment to obtain the final result – identified faults of the gas turbine modules (compressors, combustion chambers, turbines). A number of negative factors, which are explained in more detail below, affect the diagnosis process and make it difficult to reach a correct decision. Thus engine fault localization presents a challenging recognition problem.
A review of works on condition monitoring and fault detection [see 1-3,8] reveals that simulation of diagnosed systems is an integral part of their diagnostic process. The models fulfill here two general functions. The first one is to give a gas turbine performance baseline in order to calculate differences between current measurements and such a baseline. These differences (or residuals) depend little on variations of an operational mode and thus serve as reliable degradation indices. The second function is related to fault simulation. The models connect different module degradation mechanisms and the mentioned residuals, assisting in this way with a fault class description.
In first gas turbine health monitoring systems, any use of complex statistical recognition methods was too expensive in time and computer capacity. Therefore it was often decided to reduce processing requirements by simplifying diagnostic techniques. For example, Saravanamuttoo and MacIsaac [3] proposed the the diagnosis by fault matrices where every class (fault signature) is represented by residual’s signs only. Other example of a simplified technique can be found in the paper by Pipe [4]. To reduce processing requirements, the author minimizes an axis set of the class’s recognition space. Both simplifications result in losses of available information that always lead to recognition errors. Our statistical simulations of the diagnosis process have shown [see 5] that these errors can be great.
Significant advances in instrumentation and computer technology over recent years have resulted in incremental application of such innovative recognition tools as artificial neural networks. For example, Roemer and Kacprzynski [2] proposed techniques based on non-linear gas path models, statistical neural networks, and probabilistic fault identification that promise high confidence. Unfortunately, that work, as many others, lacks a numerical estimation of the method’s effectiveness and a comparison with other known techniques.
Our recent researches [for instance, 6,7] also involve non-linear gas turbine models - static and dynamic - for simulating gas path faults and neural networks for recognizing the faults. In contrast to the investigations cited previously, we approach the problem of gas turbine diagnosis reliability. Paper [6], for example, gives a preliminary comparison of three diagnostic methods where neural networks have demonstrated high accuracy.
In present paper, we perform more thorough analysis in order to finally evaluate a networks’ diagnostic capability. Neural networks are evaluated by comparing them with Bayesian recognition on the basis of the probabilities of incorrect diagnostic decisions.
The paper has the following structure. Section 2 describes applied gas path models. In section 3, the approach is given to verify the mentioned gas turbine diagnostic methods and compute probabilistic indices of method reliability. The methods are depicted in sections 4 and 5 and compared in section 6 on basis of the reliability indices. Section 7 describes neural network application to diagnosis under transient conditions.
2. Gas path Models
A computer model can easily generate a lot of diagnostic information that would be hard and sometimes nearly impossible to gather on a real gas turbine engine. For example, engine behavior can be assessed by a model under all possible operating conditions whereas field restrictions make operation diapasons of a real engine much narrower.
As pointed before, residuals are a necessary preliminary operation for the diagnosis process [see 1,7]. They may be presented as relative changes of gas path variables
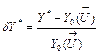 (1)
(1)
where
![]() is a measured value,
is a measured value,
![]() is a base-line value, which depends on a vector
is a base-line value, which depends on a vector
![]() of control variables (fuel consumption etc) and ambient conditions (air pressure, temperature, and humidity). Hence, a vectorial function
of control variables (fuel consumption etc) and ambient conditions (air pressure, temperature, and humidity). Hence, a vectorial function
![]() that unites the residuals for all measured variables may be interpreted as a model of normal gas turbine behavior.
that unites the residuals for all measured variables may be interpreted as a model of normal gas turbine behavior.
There can be two options to compose such a normal state model: any abstract function and a physical model. The second order four arguments full polynomial is able to correctly describe engine behaviour [see 7] and provides an example of abstract function. To compute a priori unknown coefficients, this model needs to be identified on plenty of registered data within a wide range of operational conditions.
The option of a physical model can be presented by the non-linear thermodynamic model [see 3, 8], in which every module is described by its performance map. Due to the objective physical principles implemented the model has a capacity to reflect the normal engine behaviour. Moreover, since the faults affect the module performances involved in the calculations, the thermodynamic model is capable to simulate gas turbine degradation.
To this end, the model includes correction factors
![]() that permit to displace the module maps of performances and in this way take into account a fault severity growth. Consequently, the thermodynamic model presents a vector function
that permit to displace the module maps of performances and in this way take into account a fault severity growth. Consequently, the thermodynamic model presents a vector function
![]() , which is computed as a solution of the algebraic equations system reflecting the conditions of gas turbine modules' combined work.
, which is computed as a solution of the algebraic equations system reflecting the conditions of gas turbine modules' combined work.
In addition to the thermodynamic model, a linear model
![]() (2)
(2)
is widely used in diagnostics. It connects small relative changes
![]() of the correction factors with relative deviations
of the correction factors with relative deviations
![]() of gas path variables by a matrix H of influence coefficients.
of gas path variables by a matrix H of influence coefficients.
Changes
![]() introduced into a model – nonlinear or linear - for fault simulating produce the corresponding deviations
introduced into a model – nonlinear or linear - for fault simulating produce the corresponding deviations
![]() . What is the difference between these simulated deviations
. What is the difference between these simulated deviations
![]() and the residuals
and the residuals
![]() based on real measurements? Ideally, they should be equal; however, every vector has its own errors.
based on real measurements? Ideally, they should be equal; however, every vector has its own errors.
This paper accepts the hypothesis that the model adequately describes the mechanisms of gaspath deterioration; consequently, the vector
![]() is free of errors. With respect to the vector
is free of errors. With respect to the vector
![]() , its errors occur due to measurement errors in
, its errors occur due to measurement errors in
![]() and
and
![]() as well as possible inherent inaccuracy of the function
as well as possible inherent inaccuracy of the function
![]() . It is supposed that a systematic component of total errors does not depend on a deterioration development and a random component is normally distributed.
. It is supposed that a systematic component of total errors does not depend on a deterioration development and a random component is normally distributed.
3. Common Approach to Diagnosis Reliability Estimation
In addition to forming a classification and a class recognizing, a total diagnosis process supposes an important stage of reliability estimating. The description below places emphasis on this stage.
Since an existing variety of the faults is too great to distinguish them, the faults should be divided into limited number of classes. However, real faults appear rarely and their displays depend on a fault severity, engine type, and operational conditions. For this reason, a model-based classification is formed. It is widely used in gas turbine diagnostics [see, for example, 8].
In this paper, the thermodynamic model is used to describe the faults. Then the fault classification is drawn up in the space
![]() of normalized residuals
of normalized residuals
![]() (3)
(3)
Here
![]() is a random error amplitude of the deviations
is a random error amplitude of the deviations
![]() and m is a number of analyzed variables. A vector
and m is a number of analyzed variables. A vector
![]() corresponding to the measurement
corresponding to the measurement
![]() is formed in the same way as the vector
is formed in the same way as the vector
![]() .
.
The hypothesis is accepted that an engine state D can belong to only one of q previously determined classes
![]() . The classes are constructed and the diagnosis process goes in the space of residuals (3).
. The classes are constructed and the diagnosis process goes in the space of residuals (3).
Two types of classes are concerned: single and multiple. The single type class has one independent parameter of fault severity, e.g. one correction factor or some correction factors changed proportionally. This type is convenient to describe any well-known faults of variable severity. In contrast to the single type class, the multiple type class has more than one independent parameter, e.g. some correction factors. This class type may be useful to combine some faults (for instance, the faults of one component) when their own displays and descriptions are uncertain.
A nomenclature of possible diagnosis
![]() corresponds with the accepted classification
corresponds with the accepted classification
![]() . To make a diagnosis d, a method dependent criterion
. To make a diagnosis d, a method dependent criterion
![]() is introduced as a closeness measure between a current residual vector
is introduced as a closeness measure between a current residual vector
![]() (pattern to be recognized) and every item Dj
of the classification. A decision rule
(pattern to be recognized) and every item Dj
of the classification. A decision rule
![]() (4)
(4)
is then established.
Various negative factors affect the diagnosis process and the final diagnostic decision d. In order to ensure the diagnosis d, it needs to be accompanied by any confidence assessment.
For this reason, mean probabilistic confidence characteristics are computed for the examined methods by a statistical testing procedure. Inside this procedure, numerous cycles of a method action are repeated. In every cycle, the procedure generates random numbers of the current class, fault severity, and measurement errors according to the chosen distribution laws, then computes actual pattern
![]() , and finally makes a diagnostic decision d corresponding to this pattern. A
, and finally makes a diagnostic decision d corresponding to this pattern. A
![]() diagnosis matrix Dd accumulates diagnostic decisions according to the rule
diagnosis matrix Dd accumulates diagnostic decisions according to the rule
![]() . All simulated patterns
. All simulated patterns
![]() compose a testing set
compose a testing set
![]() of a volume Nt corresponding to the total number of cycles.
of a volume Nt corresponding to the total number of cycles.
After testing cycles and diagnosis accumulation are over, the matrix Dd is transformed into a diagnosis probability matrix Pd of the same format by a normalization rule
![]() (5)
(5)
The diagonal elements
![]() present indices of distinguishing possibilities of the classes. Quantities
present indices of distinguishing possibilities of the classes. Quantities
![]() (6)
(6)
make up a vector of false diagnosis probabilities
![]() . A scalar
. A scalar
![]() that is computed as a mean number of the probabilities (6) characterizes the total level of diagnosis errors. The indices
that is computed as a mean number of the probabilities (6) characterizes the total level of diagnosis errors. The indices
![]() and
and
![]() will be applied below to adjust and compare recognition techniques under the following common conditions.
will be applied below to adjust and compare recognition techniques under the following common conditions.
A. Gas turbine operational conditions: 11 gas turbine modes established by different compressor rotation speeds under standard ambient conditions are analyzed. The most of calculations are executed for the maximal power mode called regime 1.
B. Measured parameters’ structure and accuracy correspond to a gas turbine regular measurement system which includes 6 gaspath variables. The fluctuations of the residuals (2) based on the measured parameters are assumed to be normally distributed.
C. Classification parameters.
Two classification variations are considered. The first incorporates nine single classes and every one is constituted by a variation
![]() of one correction factor. The second includes four multiple classes corresponding to the main modules (compressor, combustion chamber, compressor turbine, free turbine). Every multiple class is formed by independent variations of two correction factors of the same engine module and describes possible faults of the module. All variations
of one correction factor. The second includes four multiple classes corresponding to the main modules (compressor, combustion chamber, compressor turbine, free turbine). Every multiple class is formed by independent variations of two correction factors of the same engine module and describes possible faults of the module. All variations
![]() , which represent here fault severities, are uniformly distributed within the interval [0, 5%]. A priory probability of the classes also has a uniform distribution, so every class is equally probable.
, which represent here fault severities, are uniformly distributed within the interval [0, 5%]. A priory probability of the classes also has a uniform distribution, so every class is equally probable.
D. Testing set volume. The number Nt is chosen as a result of trade-off between a time T to execute the procedure and a computational precision of the described indices. In any case, uncertainty in the probabilities should be less than the studied effects of the method replacement or changes in diagnosing conditions. Analysis of an averaged probabilities precision helped to establish the set volume as a function of class number: Nt = 1000q.
In the next two sections, two algorithms corresponding to the mentioned methods are considered for gas turbine diagnosis. The first is based on the Bayesian approach and needs that every class be described by its probability density function. The second employs the neural networks and implies class representation by a sample of patterns.
4. Algorithm 1: Bayesian Recognition
For actual measurement
![]() and corresponding
and corresponding
![]() the Bayes formula defines a posteriori probabilities:
the Bayes formula defines a posteriori probabilities:
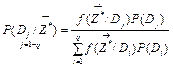 (7)
(7)
where P(Dj) is a priory probability of the class Dj and
![]() is its pattern density function.
is its pattern density function.
Density function assessment is a principal problen in statistics. To simplify it in the presented investigation, the function
![]() is determined by elemental distributions
is determined by elemental distributions
![]() and
and
![]()
![]() . (8)
. (8)
Additionally, the following assumptions were made: 1) adequacy of the linear model (2) applied to simulate faults, 2) uniform distribution
![]() of the model values
of the model values
![]() with a different fault severity, 3) normal distribution
with a different fault severity, 3) normal distribution
![]() of residual errors.
of residual errors.
According to the Bayesian rule, the recognition decision
dl is made when
![]() is maximal in the set
is maximal in the set
![]() , j=1-q. This rule corresponds with the general rule (4).
, j=1-q. This rule corresponds with the general rule (4).
The diagnostic algorithm based on the Bayesian recognition (algorithm 1) has been elaborated and inserted into the testing procedure described above.
As noted above, the Bayesian recognition is not without its difficulties. Only the simple structure classes that are based on the linear model and ordinary theoretical distributions can be analyzed. That is why a class representation directly by the patterns of measured variables is considered too, as well as algorithm 2 that is capable of treating them.
5. Algorithm 2: Neural Networks
The representation by the patterns permits simulating the fault classes of complex structure. For instance, a nonlinear thermodynamic model can be used, and the classes described by three and more correction factors can be analyzed. Furthermore, this permits direct forming the real data-based classes, without any model assistance and consequently without negative influence of model proper errors.
To solve difficult pattern recognition problems, a multilayer perceptron is successfully applied [see 9, 10], since a back-propagation algorithm has been proposed to train them. That is why back-propagation networks were chosen for gas turbine diagnosis. The employed networks have the structures that are partially determined by the measurement system and fault classification compositions.
The input layer incorporates six nodes, which correspond to a residual vector dimension. The output layer points to the concerned classes and therefore includes nine elements for the single type classification and four elements for the multiple one.
Within the statistical testing procedure, the described network passes training and verification stages. To train neural networks, a reference set
![]() of the volume Nr = 1000q is composed in the same manner as the testing set
of the volume Nr = 1000q is composed in the same manner as the testing set
![]() . The verification stage follows then, at which the probabilities
. The verification stage follows then, at which the probabilities
![]() and
and
![]() (error probabilities) are computed on the testing set.
(error probabilities) are computed on the testing set.
The testing procedure was repeated many times in order to choose the best parameters of the classification and network, namely a reference set volume, hidden layer size, training algorithm variation, and training algorithm epoch number. It was also established that one hidden layer of 12 nodes is the most appropriate and the epoch number 200 guarantees a network complete training as well as absence of the over-teaching.
To sum up sections 4 and 5, two approaches to gas turbine diagnosis were adopted and statistically tested by the procedure described above.
6. Comparison of the Algorithms
Since the Bayesian recognition (algorithm 1) minimizes average false recognition probabilities [see, for example, 11], it is used as a standard technique for evaluating algorithm 2. The algorithms comparison is conducted for two classification variations as described in section 3.
Table 1 contains the resulting probabilities
![]() and helps to estimate averaged diagnosis errors for the compared algorithms. As can be seen, the probability differences between the algorithms, - 0.050 for single type classification and +0.037 for the multiple type classification, are noticeably lower then probability levels.
and helps to estimate averaged diagnosis errors for the compared algorithms. As can be seen, the probability differences between the algorithms, - 0.050 for single type classification and +0.037 for the multiple type classification, are noticeably lower then probability levels.
Table SEQ Table \n 1. Mean probabilities of false diagnosis
Algorithms |
Type of classes |
|
Single |
Multiple |
|
Bayesian approach |
0.1822 |
0.1256 |
Neural networks |
0.1772 |
0.1293 |
Difference |
-0.0050 |
0.0037 |
More detailed analysis can be performed with the probabilities that are individual for every class, i.e. vector
![]() elements. The probability shifts induced by the change from algorithm 1 to algorithm 2 are given in Table 2. It can be seen that the differences in false probabilities between the algorithms are slight for all classes. Average absolute shifts
elements. The probability shifts induced by the change from algorithm 1 to algorithm 2 are given in Table 2. It can be seen that the differences in false probabilities between the algorithms are slight for all classes. Average absolute shifts
![]() for single and multiple classes are 0.014 and 0.007 correspondingly.
for single and multiple classes are 0.014 and 0.007 correspondingly.
To ensure the results and preliminary conclusions, the statistical testing procedure with algorithm 2 was repeated 10 times (option of the single type classification) with different random number series. As a result, average values M(P) and standard deviations s(P) of the error probabilities have been computed. The resulting statistics are placed in Table 3. Comparing tables 2 and 3 it can be seen that differences in diagnosis accuracy between the analyzed algorithms are smaller then inaccuracy intervals.
Table SEQ Table \n 2. False probabilities' shift for algorithm 2
Indices |
Type of classes |
||
Single |
Multiple |
||
|
|
+0.021 |
-0.005 |
|
+0.011 |
-0.002 |
|
|
+0.008 |
+0.012 |
|
|
-0.005 |
+0.010 |
|
|
+0.001 |
- |
|
|
-0.002 |
- |
|
|
-0.023 |
- |
|
|
-0.039 |
- |
|
|
-0.022 |
- |
|
|
0.014 |
0.007 |
Table SEQ Table \n 3. Statistical parameters of the error
probabilities (stationary case)
Stati-stics |
|
|
||||||||
d1 |
d2 |
d3 |
d4 |
d5 |
d6 |
d7 |
d8 |
d9 |
||
M(Pe) |
0.283 |
0.270 |
0.221 |
0.423 |
0.215 |
0.020 |
0.222 |
0.225 |
0.227 |
0.234 |
s(Pe) |
0.017 |
0.015 |
0.010 |
0.031 |
0.011 |
0.004 |
0.013 |
0.012 |
0.017 |
0.004 |
To make a broader conclusion about network effectiveness, in addition to the previous calculations executed for the mode 1, the statistical testing and method comparison were repeated for the other operating points. The results were very similar: algorithm 2 was always close to the algorithm 1.
Thus, we arrive at an important conclusion that artificial networks do not practically yield to the Bayesian approach when applied to gas turbine diagnosis. These positive results of network evaluation under steady state conditions encouraged us to develop a network-based diagnosis algorithm for transient conditions [12]. With respect to the Bayesian approach, it seems to be too difficult to compute integral (8) at transients.
The next section describes conditions and the accuracy analysis of diagnosis at transients.
7. Network Application for Transient Conditions
Extending the explanation given in section 3 for steady states, a generalized deviation vector
![]() is determined under dynamic conditions as follows. Transients of normal (healthy) and faulted engines are divided into time-points. The deviations are determined on the next step for every pair of similar points of “faulted” and “normal” trajectories; errors are added then. Finally, the generalized vector
is determined under dynamic conditions as follows. Transients of normal (healthy) and faulted engines are divided into time-points. The deviations are determined on the next step for every pair of similar points of “faulted” and “normal” trajectories; errors are added then. Finally, the generalized vector
![]() is composed from all successive deviations of trajectory points.
is composed from all successive deviations of trajectory points.
In the actual analysis, seven variables are monitored. A transient trajectory includes 14 time-points. The vector
![]() , a pattern to be recognized, consists of 14´7=98 elements. The classification consists of eight single faults classes. The optimal hidden layer number is 25. So, the network has a structure "98×25×8". Other conditions of the analysis, including pattern number 1000 to describe one class, are equal to the conditions given in sections 3 and 5.
, a pattern to be recognized, consists of 14´7=98 elements. The classification consists of eight single faults classes. The optimal hidden layer number is 25. So, the network has a structure "98×25×8". Other conditions of the analysis, including pattern number 1000 to describe one class, are equal to the conditions given in sections 3 and 5.
A calculation under the noted computational conditions called a basic calculation has acceptable execution time of 8 minutes (PC with Pentium IV). A mean probability of the correct diagnosis works out at 0.886 (error probability 0.114) for this calculation.
As before in the case of static conditions, the basic calculation was repeated 10 times with different random number series. New average values M(P) and standard deviations s(P), which characterize a computational inaccuracy at transients, are placed in Table 4. Comparing tables 3 and 4, it can be seen that reduction in diagnosis inaccuracy is considerable for every class and in general: the average losses decrease in two times. This positive effect is considerably greater than the computational inaccuracy.
In addition to the basic calculation, 15 different calculations at different transient conditions (engine acceleration or deceleration, transient profile, ambient air temperature) were made. The obtained probability of the correct diagnosis worked out at 0.896-0.841 (on average 0.876).
In general, it can be stated that neural networks application for diagnosis under transient conditions enhances essentially the gas turbine diagnosis reliability.
Table 4. Statistical parameters of the error
probabilities (transient case)
Stati-stics |
|
|
|||||||
d1 |
d2 |
d3 |
d4 |
d5 |
d6 |
d7 |
d8 |
||
M(Pe) |
0.081 |
0.193 |
0.082 |
0.189 |
0.089 |
0.104 |
0.100 |
0.108 |
0.118 |
s(Pe) |
0.09 |
0.015 |
0.018 |
0.023 |
0.006 |
0.012 |
0.009 |
0.013 |
0.003 |
Conclusions
In this paper, a statistical testing has been discussed of gas turbine diagnosis by means of neural networks and the Bayesian recognition. A thermodynamic model served to simulate gas turbine degradation and form a faults classification. The purpose was to compare neural networks with the Bayesian recognition using the latter as a standard technique with limit properties. Diagnosis reliability indices - averaged probabilities of true/false diagnosis – were criteria of the comparison.
The diagnosis algorithm applying back-propagation networks has demonstrated a high reliability. Tt was quite close to the algorithm based on the Bayes formula in different conditions of application.
On basis of common approach to gas turbine diagnosis involving artificial neural networks, a new diagnostic algorithm has been developed to be applied at transients. During the experimentation a reachable accuracy level of gas turbine diagnosis was estimated. It was pointed out that the change to the diagnosis at transient can reduce false diagnoses in two times.
So, neural back-propagation networks can be recommended for a practical use in condition monitoring systems both at steady states and at transients. Since the Bayesian approach has an advantage of accompanying every diagnosis by its probability, this approach may also be recommended when we are able to describe the fault classes by their density functions.
Acknowledgments
The work has been carried out with the support of the National Polytechnic Institute of Mexico (project 20070707).