Gas Turbine Diagnostic Model Identification On Maintenance Data Of Great Volume

This paper deals with an identification procedure of gas turbine nonlinear models for monitoring and diagnostic systems. Introduction of a special time variable into a conventional thermodynamic model helps to create a model of the engine with a variable deterioration level. To identify this model, registration data of great volume and different gas turbine deterioration severity can be attracted. This ensures high accuracy of the identified model as well as quality of a baseline function that can simply be extracted from the model.

Gas turbine thermodynamic model, model identification, deviations of measured variables, identification accuracy

1. Introduction

Design of a gas turbine itself and its systems is deeply related with calculations on the base of gas path mathematical models of different complexity. A health monitoring system is an integral part of a modern gas turbine; it is applied not only for maintenance needs but for aims of gas turbine development ant tests as well. In such systems, nonlinear static gas path models, also called thermodynamic models, are widely used to simulate engine operation at steady states. This is explained by high cost of physical fault simulation, an infrequent display of the faults at real engines, and other causes.

In thermodynamic models, gas path variables (pressures and temperatures of air or gas, rotor speeds, etc) are in relation with atmospheric conditions, engine control variables, and special internal parameters (correction factors). The latter parameters are able to displace performance maps of engine components (compressors, turbines, combustion chamber, etc) simulating their degradation by such a way.

Last computer progress stimulates an application of sophisticated elements in monitoring systems, such as thermodynamic model identification procedure considered in this paper. Identification represents an effective technique of model accuracy enhancement. During the identification such correction factors are determined which minimize the distance between the model gas path variables and the measured ones. Besides the better model accuracy, the simplification of the diagnosing process is reached because the found estimations of the correction factors contain information of a current technical state of the components.

The diagnostic algorithms based on the model identification constitute a separate approach in gas turbine diagnostics [1-7]. The researchers involve different mathematical methods, for instance, weighted-least-squares [6] and Kalman filter [7]. Aretakis et al. [5] proposed and use a combinatorial approach in order to get the estimations when input information is limited. When the researchers have in their disposal the data registered through a prolonged period, they usually calculate successive estimations and analyze them in time [3,8].

In paper [9], we proposed a gas path polynomial model that takes gradual engine performance degradation in consideration. That model has an additional argument, time variable, and can be identified on registered data of great volume. If we put the time variable equal to zero, the model will be transformed into a good baseline function for diagnostic algorithms.

In the present paper, this idea is developed in application to the thermodynamic model. Two purposes are achieved by such model identification. The first purpose consists in creating the model of a gradually degraded engine while the second is to have a baseline function of high accuracy. The idea is verified on maintenance data of a stationary gas turbine power plant.

2. General Thermodynamic Model Identification Procedure

A diagnostic process generally includes a stage of computing deviations

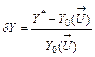,                   (1)

between a measured gas path variable  and a baseline function  of a healthy engine. The function arguments are united in a vector  of operating conditions (atmospheric conditions and engine control variables).

The deviations  are practically free of an influence of operating conditions and may serve as good degradation indicators. However, a lot of negative factors affect the deviation accuracy masking the degradation effect. The most of them are related with the function .

It is known that the gas turbine power and climatic curves are smooth. As shown in paper [10], these curves can be well described by a second order full polynomial of four arguments

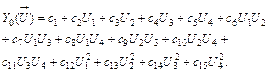  (2)

Consequently, this polynomial is a good baseline function.

Paper [10] also proves that the thermodynamic model can be used as an engine baseline function. According to the previous explanations, this model has a structure

                             (3)

and relates the gas path variables  with the operating conditions  and corrections factors . The model (3) is computed as a solution of the system of algebraic equations reflecting the conditions of the components combined work at steady-state regimes.

Every factor  is defined as a relative change

                            (4)

of an actual component performance map parameter  (corrected flow parameter or efficiency parameter of an analyzed component) from its nominal value . If vector  of fixed correction factors corresponds to a healthy engine, the baseline can be presented by an expression

.                        (5)

The measured values  of a healthy engine differ from the model-generated values  due to the model errors  and the measurement errors , therefore . Identification of model (5) permits to reduce considerably its errors  in despite of the measurement errors of the data used. Such estimations  are determined that minimize a distance  between model values and measured values:

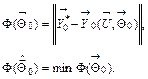                 (6)

Accuracy of an identified baseline model

                          (7)

depends on a volume of a learning sample with the measured values used for the identification. For better identification accuracy, the learning sample generally incorporate measurements from different engine operating points (operating modes).

The learning sample problem seems to be challenging. On the one hand, the learning sample must be representative and incorporate the data collected in all passable operation regimes and at different ambient conditions. On the other hand, maintenance conditions do not permit arbitrary changes of an engine operating mode. Moreover, a data collection period is limited by a short time when a gas turbine state can be considered as healthy and invariable.

To overcome the mentioned difficulties, we propose to introduce a time variable into the model (3) and identify such a model on all available maintenance data of variable engine degradation. The identified model will take into consideration a degradation effect. To get a baseline model, the time variable should be fixed. The next section describes details of this approach.

3. Model Identification Details and Input Data Preparation

The idea to introduce a time variable into the gas turbine model and identify such model was firstly verified in our papers [9,10]. We proposed a new structure of the polynomial model

,             (8)

which is based on baseline function (2). The baseline  obtained through identification of model (8) have demonstrated notable enhancement and was recommended for health monitoring systems [9].

In these systems, the thermodynamic model is widely used as well. It has some advantages relatively polynomial model. First, model (3) is capable to simulate different faults and is used in many fault localization algorithms. Second, the model can evaluate some important engine performances inaccessible or difficult for direct measurement, such as an engine power and total efficiency. Third, model (3) is physics-based and conserves after the identification its correct behavior in all operating conditions while the polynomial model is adequate only around the points of the learning sample. That is why the thermodynamic model with a time variable and the corresponding identification procedure are considered below.

We attempted to introduce the time corrections into the thermodynamic model variables according to formula (8) however the identification procedure was not stable. Moreover, this mode is not too physical. Every gas path variable is adjusted independently while real engine degradation changes the variables in certain proportion.

The next attempt, when we introduced the time variable into component performance description, was successful.

It follows from (3) that

                        (9)

in the original identification procedure while, in the modified procedure, a new performance description

                   (10)

is applied, where  is a relative time. This expression corresponds to a linear influence of an engine operation time on degradation severity.

To identify the thermodynamic model with the time variable introduced according to formula (10), maintenance registration of a power plant with a free turbine is used. The registration covers the periods of axial compressor fouling, subsequent cleaning, and next fouling. These data present important information for the diagnostics because the fouling can be classified as one of the most frequent gas turbine faults. In the used database, gas path variables and operating conditions were registered within an hour interval.

Two learning samples have been formed: sample 1 of 3800 operating points (t = 3800 hours) and sample 2 of the first 1800 points (t = 1800 hours). The latter sample is concerned because the fouling effect is practically linear here and the model with a linear degradation mechanism can be identified perfectly. The cleaning takes place after the time point t = 906. The power plant condition in this point is considered as normal and the relative time  is equal to zero. In the point t = 3800, the variable  has its maximal value 0.7235. In the interval before the cleaning, the relative time  varies from 0.1165 to 0.3430 according to the fouling severity in this interval.

Other identification conditions, equal for the both samples, are: number of the measured gas path variables is six; number of the estimated correction factors varies from 7 to 11 and Table 1 specifies them. Three mechanical components (compressor, compressor turbine, and power turbine) are examined here and two parameters , flow factor and efficiency factor, are generally introduced for every component (parameters from 3 through 8 in the table). Additional parameters 1 and 2 are introduced to take into account different compressor performance shifts at low and high rotation speeds. Moreover, parameters 9-11 are included in order to simulate compressor deterioration according to expression (10).

Table 1. Correction factors used

№

Desig-nation

Factor’s name

1

GCn1

Compressor corrected air flow (low speed)

2

GCn2

Compressor corrected air flow (high speed)

3

GC

Compressor corrected air flow

4

ηC

Compressor efficiency

5

AT

Turbine corrected gas flow

6

ηT

Turbine efficiency

7

APT

Power turbine corrected gas flow

8

ηPT

Power turbine efficiency

9

πCt

Compressor pressure ratio (time variable)

10

GCt

Compressor corrected air flow (time variable)

11

ηCt

Compressor efficiency (time variable)

The next section describes the results of the thermodynamic model identification by the original and modified procedures.

4. Results of the Model Identification on Maintenance Data

The estimations  of correction factors for two procedures and two input data samples mentioned above are placed in Table 2. It can be seen that the differences between the concerned cases are not too great for all factors. With respect to parameters πCt, GCt, and ηCt responsible for the degradation simulation, the have physically acceptable values. We can also add that the modified procedure had no difficulties to estimate 11 correction factors while the original procedure was sometimes unstable in this case.

To verify better the identification quality, deviations (1) between the learning sample data and the thermodynamic model are graphically analyzed below. Deviation plots are constructed for four cases: before the identification, after the identification by the original procedure, after the identification by the modified procedure when the time variable is switched off, and after the identification by the modified procedure when the variable is switched on.

We will firstly analyze sample 1 (3800 time points) by the example of a high pressure turbine temperature. Figure 1 shows its deviations  in the form of time plots for the mentioned four cases. The following can be stated after the plot analysis. 1) The trends provoked by the fouling and the cleaning-induced shifts are well distinguishable. The deviation quality (signal-to-noise ratio) is lower in the right part of the plots. Some causes of the disturbances - in particular, measurement latent defects that are not distinguishable by common filtration methods - have been determined in our papers [10,11]. The factors that influence the engine but are not taken into account in the model yet - for example, air humidity – can also affect the deviations. 2) The modified procedure is not worse than the original one by the deviation quality (compare plots “b” and “c” of Fig.1). 3) The deviations computed relatively the model with time variable (see plot “d”) should contain only random fluctuations if the model is adequate to registered data. However, it can be concluded that the deviation still contain remaining effects of the fouling and clearing.

Table 2. Estimations of the correction factors

Procedure

GCn1

GCn2

GC

ηC

AT

ηT

APT

ηPT

πCt

GCt

ηCt

Original (samples 1,2)

-.0971

-.0122

-

.0714

.0293

-.0974

.0666

.0279

-

-

-

Modified (sample 1)

-.0971

-.0122

.0281

.1056

.0146

-.1179

.0633

.0196

-.1262

-.0493

-.0487

Modified (sample 2)

-.0971

-.0122

.0407

.0973

.0333

-.1067

.0723

.0311

-.0765

-.1043

-.0658

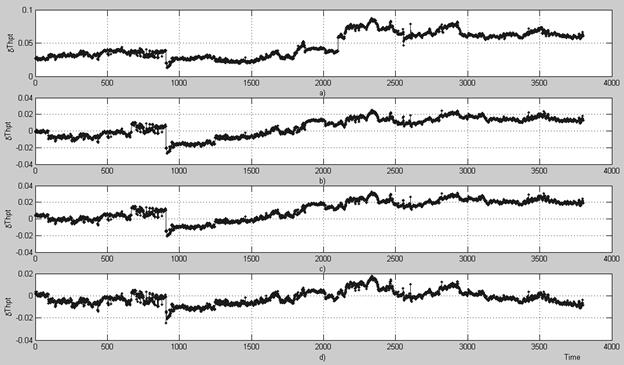
Fig. 1. High pressure turbine temperature deviations for Sample 1

(a – before the identification; b – after the identification by the original procedure; c – after the identification by the modified procedure when the t-variable is switched off; d – after the identification by the modified procedure when the t-variable is switched on)

The noted above difficulties of the proposed identification mode should be additionally analyzed. That is why we repeat the previous analysis for sample 2 of 1800 time points. The corresponding deviation plots  are constructed in Fig.2 for the same four cases as before. Comparing plots “c” and “b”, slight enhancement of the modified procedure relatively the original one can be noted. It can also be seen that the deviations of plot “d” are practically free of the fouling and clearing influence.

Figure 3 shows the deviation plot  for other measured variable, pressure behind the high pressure turbine. Comparing this figure with Fig.2 we can conclude that the deviation disturbances and plot “d” fouling and clearing effects are slightly greater for the pressure variable than for the temperature variable.

Summing up the analysis of the presented deviation plots as well as the analysis of the other monitored gas path variables, we can state that the presented mode of the thermodynamic model identification has demonstrated a slightly higher accuracy. It is also capable to determine greater number of the correction factors and additionally enhance the model in this way. The analysis has demonstrated as well that the investigation should be continued.

Conclusions

A new mode has been proposed of the thermodynamic model identification on great volume registered data with different gas turbine degradation severity. To take into account a variable fouling level, a time variable was introduced into compressor performance description.

Comparison of the modified identification procedure with the original one was made by means of deviation time plots constructed for different data samples. The comparison has shown that the proposed identification mode has better properties.

The obtained model taking into account variable gas path deterioration can be successfully applied in gas turbine monitoring, diagnostics, and prognostics. Moreover, this model can be simply converted into a baseline model of a high quality. Such a model can be widely used in monitoring systems as well.

This paper, however, can be considered only as the first attempt to identify the thermodynamic model on the data of different gas turbine degradation severity. We shall continue our investigations.

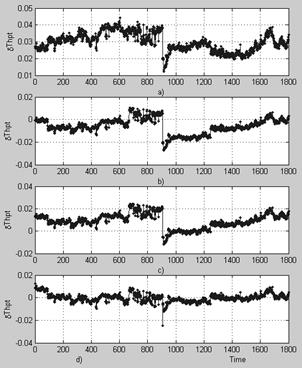
Fig. 2. High pressure turbine temperature deviations for Sample 2 (see in Fig.1 the explanations for plots “a”, “b”, “c”, and “d”)

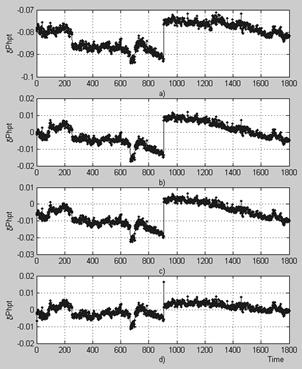
Fig. 3. High pressure turbine pressure deviations for Sample 2 (see in Fig.1 the explanations for plots “a”, “b”, “c”, and “d”)

Acknowledgments

The work has been carried out with the support of the National Polytechnic Institute of Mexico (project 20070707).