Reliability Enhancement Of Gas Turbine Fault Identification
Main focus of this paper is a reliable fault identification of gas turbines. The paper examines the methods of gas turbine parametric diagnosing. The nonlinear thermodynamic model describes different gradually developing faults. To identify them, the method operation is simulated in the conditions of random measurement errors, the correct and incorrect diagnostic decisions are fixed, and corresponding averaged probabilities are computed. The objectives are to verify the methods statistically, adjust them, and choose the best one which ensures the higher probability of fault correct identification. Besides the method comparison, the paper also considers a problem of classifying the various gas turbine faults. Different classification variants are presented to make more general the analysis of diagnosing process. A generalized fault classification which unites the fault descriptions from different operational regimes is also proposed and analyzed. It conserves a trustworthiness level of the previous regime dependent classification and makes the diagnosing be much more universal.
gas turbine fault classification, thermodynamic model, gas turbine diagnosing methods, statistical verification of the methods, fault identification trustworthiness
1. Introduction
For a new generation of high temperature and high output gas turbines the objectives of a high availability and limiting degradation is very important and advanced condition monitoring systems for turbomachines and auxiliary equipment are designed and maintained recent decades.
To resolve different deterioration problems, a monitoring system must incorporate a variety of technologies including a gaspath analysis also known as aerothermal or thermodynamic performance analysis [6]. Gaspath analysis of turbomachinery presents an advanced calculation technique capable to compute and correlate all performance variables of the gaspath and, in this way, relate fault parameters with measured variables. So, this technology permits to simulate and detect the faults. Diagnosing based on gaspath analysis incorporates three interrelated approaches: common monitoring of engine health, health prognostics, and concerned in this paper detailed diagnostics (fault identification or localization) [10].
Although the faults exert influence on measured and registered gaspath variables (pressures, temperatures, rotation speeds, and so on), the impact of changes in operational regime is much greater and they hide fault effects. That is why in diagnosing algorithms, raw measurement data should be subjected to a complex mathematical treatment to obtain final result – identified faults of gas turbine modules (compressors, combustors, turbines). A lot of negative factors, which are explained in more detail below, affect the diagnosing process and make difficulties for the correct decision. So, engine fault identification presents a challenging problem.
Reviewing works on condition monitoring and fault detection [see 1, 6, 7] it can be stated that a simulation of analyzed systems is an integral part of their diagnostic process. The models fulfill here two general functions. The first one is to give a gas turbine performance baseline in order to calculate differences between it and current measurements. These differences (or residuals) do not practically depend on operational regime variations and so serve as good degradation indices. The second function is related with a fault simulation. The models connect different module degradation mechanisms and the residuals assisting with a fault class description.
In first gas turbine health monitoring systems, any use of complex statistical recognition methods was too expensive in time and computer capacity. Therefore it was often decided to reduce processing requirements by a diagnostic techniques simplification. For example, Saravanamuttoo and MacIsaac [8] proposed the diagnosing by fault matrices where every class (fault signature) is presented by residual’s signs only. Other example of a simplified technique can be found in the paper by Pipe [5]. To reduce processing requirements, the author minimizes an axis set of the class’s recognition space. Both mentioned simplifications mean losses of available information that always provoke recognition errors and our statistical simulations of diagnosing process have shown [see 11] that these errors are great.
Significant advances in instrumentation and computer technology over recent years resulted in more perfect approaches such as the work by Roemer and Kacprzynski [7]. The techniques proposed by the authors are based on non-linear gaspath models, statistical neural networks, and probabilistic fault identification that promise high confidence. Unfortunately, that work, as many others, lacks for a numerical estimation of method’s effectiveness and any comparison with other known techniques. In contrast to the noted investigations, the presented paper focuses on the trustworthiness problem of gas turbine diagnosing.
The paper has the following structure. Section 2 describes applied gaspath models. In section 3, the approach is given to verify gas turbine diagnosing methods and compute probabilistic indices of trustworthiness. Two diagnostic methods are depicted in sections 4 and 5 and compared in the basis of the trustworthiness indices in section 6. The mode to generalize the accepted fault classification and make the diagnosing more universal is concerned in section 7. Section 8 concludes the results and discusses the perspectives of practical implementation of the presented methods in real health monitoring systems.
2. Gaspath models
A computer model can generate easily a lot of diagnostic information that would be hard and sometimes practically impossible to gather on a real gas turbine engine. For example, engine behavior can be studied by the models at all possible operating conditions whereas field restrictions make engine operation diapasons very narrow.
Residuals necessary for a diagnosing process [see 1, 4] may be presented as relative changes of gaspath variables
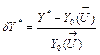, (1)
where
is measured value,
- base-line value, and the vector
unites control variables (fuel consumption and any other) and ambient conditions (air pressure, temperature, and humidity). So, the vectorial function
to compute residuals of all measured variables may be interpreted as a model of gas turbine normal behavior.
There can be two options to compose such a normal state model: any abstract function and a physical model. The second order four arguments full polynomial is able to describe correctly engine behaviour [see 4] and gives an example of abstract function. To compute a priori unknown coefficients, this model needs to be taught on numerous registered data inside a wide range of operational conditions.
The option of a physical model can be demonstrated by the non-linear thermodynamic model [8, 10], in which every module is described by its full manufacture performance map. Due to objective physical principles realized the model has a capacity to reflect the normal engine behaviour. Moreover, since the faults affect the module performances involving in the calculations, the thermodynamic model is capable to simulate gas turbine degradation.
The vector of correction factors
permits to displace the module maps of performances and in this way take into account a fault severity growth. So, the thermodynamic model presents the vector function
, which is computed as a solution of the algebraic equations system reflecting the conditions of a gas turbine modules combined work.
Any correction factor change
introduced in the model to simulate a fault produces the corresponding gaspath variable change
. What is a difference between this simulated deviations
and the residuals
based on real measurements? Ideally, they should be equal, however every vector has its own errors.
In this paper, the hypothesis is accepted that the model adequately describes the mechanisms of gaspath deterioration; consequently, the vector
does not contain errors. As regards the vector
, its errors occur due to measurement errors in
and
as well as possible inherent inaccuracy of the function
. It is supposed that a systematic component of total errors does not depend on a deterioration development and a random component is normally distributed.
3. Common approach to recognition trustworthiness estimation
In addition to a classification forming and a recognizing itself, a total recognition process supposes an important stage of trustworthiness estimating and emphasis is given on this stage in the next description of a maintained approach to gas turbine fault recognition.
Existent fault variety is too great to distinguish all possible gas turbine degradation modes and these modes should be divided into limited number of classes. However, there are difficulties to form a representative classification based on real fault appearances only: the faults appear rarely and their displays depend on a fault severity, engine type, and operational conditions. For this reason, a model-based classification widely used in diagnostics [see 9, 10] is formed.
In this paper, the thermodynamic model is applied to describe the faults. Then the classification is made up and diagnostic decisions are taken in the multidimensional space
of the normalized residuals
. (2)
Here
is the maximal random error amplitude of the deviations
and m
is a number of analyzed variables. The vector
corresponding to the measure
is formed in the same way as the vector
.
The hypothesis is accepted that an object (engine) state D can belong to one of q
determined beforehand classes
only. Every class is presented here by its sample of residuals generated by the model. Residual samples of all classes compose a reference set of a total volume Nr.
Two types of classes are concerned: single and multiple. The single type class has one independent parameter of fault severity, for example, one correction factor or some correction factors changed proportionally. This type is convenient to describe any well known fault of variable severity. In contrast to the single type class, the multiple type class has more than one independent parameter, for example, some correction factors to be changed independently. This class type may be useful to combine some faults (for instance, the faults of one component) when their own displays and descriptions are uncertain.
A nomenclature of possible diagnosis
corresponds with the accepted classification
. To make a diagnosis d, a method dependent criterion
is introduced as a closeness measure between a current residual vector
(pattern) and every item Dj of the classification and a decision rule
(3)
is established.
Various negative factors affect a diagnosing process and final recognition results and, to ensure the diagnosis d, it needs to be accompanied by any confidence assessment.
For this reason, mean probabilistic confidence characteristics are computed for examined methods by a statistical testing procedure. Inside this procedure, numerously cycles of a method action are repeated. In every cycle, the procedure generates random numbers of the current class, fault severity, and measurement errors according chosen distribution laws, then computes actual pattern
, and finally takes a diagnostic decision d corresponding to this pattern. A
diagnosis matrix Dd accumulates diagnostic decisions according the rule
. All simulated patterns
compose a testing set
of a volume Nt corresponding to the total number of cycles.
After a termination of the testing cycles and diagnosis accumulation, the matrix Dd is transformed into a diagnosis probability matrix Pd of the same format by a normalization rule
. (4)
Table 1 helps to interpret such a probability matrix. The diagonal elements
present indices of distinguishing possibilities of the classes and form a probability vector
of true diagnosis. Scalar
computed as a mean number of these elements characterizes the total controllability of the engine. Probabilities of false diagnosis
(5)
are also applied to estimate the diagnosing methods.
Table 1. Diagnosis probability matrix
Diagnosis |
Classes |
|||
D1 |
D2 |
… |
Dq |
|
d1 |
Pd11 |
Pd12 |
… |
Pd1q |
d2 |
Pd21 |
Pd22 |
… |
Pd2q |
… |
… |
… |
… |
… |
dq |
Pdq1 |
Pdq2 |
… |
Pdqq |
Two recognition techniques have been chosen for diagnosing. The first technique operates with the Euclidian distance to recognize gas turbine fault classes and the second applies the neural networks as a recognition tool. The techniques have been adapted for the diagnosing and statistically tested by the described above procedure. While the testing the settings of these diagnosing methods were adjusted and the methods were compared in equal conditions which are described below.
A. Gas turbine operational conditions: 11 gas turbine regimes established by different compressor rotation speeds under standard ambient conditions are analyzed. The most of calculations are executed for the maximal regime called regime 1.
B. Measured parameters’ structure and accuracy correspond to a gas turbine regular measurement system which includes 6 gaspath parameters. It is assumed that fluctuations of the residuals (2) based on the measured parameters are normally distributed.
C. Classification parameters.
Two classification variants are considered. The first incorporates nine single classes and every one is constituted by a variation
of one correction factor. The second includes four multiple classes corresponding to the principle modules (compressor, combustion chamber, compressor turbine, free turbine). Every multiple class is formed by independent variations of two correction factors of the same engine module and describes possible faults of the module. All variations
which present here fault severities are uniformly distributed within the interval [0, 5%]. The class probabilities also have a uniform distribution, so every class is equally probable.
D. Testing set volume. The numbers Nr and Nt are chosen as a result of compromise between a time T to execute the procedure and a computational precision of the described indices. In any case, uncertainty in the probabilities should be less than studied effects of the method replacement or changes in diagnosing conditions. Analysis of an averaged probabilities precision helped to establish the set volumes as functions of class number: Nr = Nt = 1000q.
Two following sections describe the examined diagnosing methods, explain their adjustments, and give some trustworthiness characteristics computed under the noted above conditions.
4. Method 1: Euclidian distance
There are two common forms to describe classes: by density functions and directly by measurement point (pattern) samples. Recuperation of density functions presents a principle problem of statistics and can be realized for simplified class representations. That is why in this paper, a class representation directly by pattern samples is considered as well as the methods capable to treat them.
Such a representation permits simulating a fault severity growth by an exact nonlinear thermodynamic model and forming complex multiple classes described by three and more correction factors. Furthermore, this permits forming real data based classes of general type without any model assistance and consequently without negative influence of model proper errors.
Fig. 1 and Fig. 2 illustrate the described class representation; pattern samples of four classes of single and multiple types are shown here in the three-dimensional space
. The multiple type classes seem to be more diffused and intercrossed.
Concerned method operates with a geometrical measure of closeness between the current vector
and every class Dj of the classification. This measure is based on the Euclidian distance between two points in a multidimensional space and serves as a criterion Rj to identify the proper class according the rule (3).
The computational algorithm has been realized in the testing procedure and incorporates the following items.
· A reference set
of the volume Nr incorporating the pattern samples
for all classes is composed outside the testing cycle.
· The criteria Rj are calculated for actual
of the testing set and all
of the reference set.
· The diagnosing decision dl is accepted by the rule (3).
· The trustworthiness indices (4) and (5) are calculated according to the general scheme (see section 3).
There can be different modes to compose criterion R from individual distances li: to use simple mean value M(li), to calculate mean value of inverse distances M(1/li), to apply mean value of inverse quadratic distances M(1/li2) etc. Applying of inverse distance gives a greater weight to near points of the sample
, quadratic function increases this property. In preliminary statistical testing, the criterion R=M(1/li2) ensured the best class distinguishability and has been selected for further use.
The diagnosing probabilities (4) corresponding to the operational regime 1 and single type classification are placed in Table 2. Table 3 includes the same data for the multiple type classification.
From Table 2 it can be seen that the classes D2 and D4
have the lowest distinguishability according
and the elevated magnitudes Pd42 and Pd24
explain the cause – a great mutual intersection of these classes. The class D6 has the highest distinguishability 0.985 that results from excessive method sensibility to this class to the prejudice of all other classes: the probabilities Pd6j of wrong diagnosis are too great.
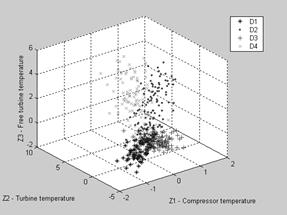
Fig.1. Classes representation by the pattern samples
(single type)
Comparing Table 2 and Table 3 it can be noted that individual (for every class, see the vector
) and total (see
) trustworthiness indices of the multiple classification are visibly greater. This is a result of two opposite tendencies. On one hand, the substitution of a single type of classes on a multiple one generally induces more close class intersection and, consequently, lower trustworthiness. On the other hand, the significant reduction of class total quantity from nine to four has a contrary influence. As can be seen, the second tendency prevails. The following diagnosing method is based on neural networks which present a fast growing computing technique expanding through many common fields of applications [6].
Fig.2. Classes representation by the pattern samples
(multiple type)
Table 2. Trustworthiness indices (single class type)
Pd |
|||||||||
Diag-nosis |
Classes |
||||||||
D1 |
D2 |
D3 |
D4 |
D5 |
D6 |
D7 |
D8 |
D9 |
|
d1 |
0.734 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.006 |
d2 |
0.0 |
0.752 |
0.0 |
0.218 |
0.016 |
0.0 |
0.001 |
0.0 |
0.0 |
d3 |
0.001 |
0.0 |
0.781 |
0.001 |
0.0 |
0.005 |
0.005 |
0.0 |
0.004 |
d4 |
0.0 |
0.030 |
0.0 |
0.610 |
0.001 |
0.0 |
0.0 |
0.0 |
0.0 |
d5 |
0.0 |
0.009 |
0.0 |
0.013 |
0.776 |
0.0 |
0.0 |
0.001 |
0.0 |
d6 |
0.152 |
0.127 |
0.216 |
0.092 |
0.156 |
0.985 |
0.180 |
0.241 |
0.204 |
d7 |
0.0 |
0.029 |
0.0 |
0.019 |
0.010 |
0.001 |
0.788 |
0.001 |
0.0 |
d8 |
0.0 |
0.053 |
0.003 |
0.047 |
0.041 |
0.009 |
0.026 |
0.757 |
0.001 |
d9 |
0.113 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.785 |
|
|||||||||
0.734 |
0.752 |
0.781 |
0.610 |
0.776 |
0.985 |
0.788 |
0.757 |
0.785 |
|
|
Table 3. Trustworthiness indices (multiple class type)
Pd |
||||
Diag-nosis |
Classes |
|||
D1 |
D2 |
D3 |
D4 |
|
d1 |
0.763 |
0.002 |
0.007 |
0.001 |
d2 |
0.109 |
0.623 |
0.002 |
0.005 |
d3 |
0.081 |
0.088 |
0.949 |
0.045 |
d4 |
0.047 |
0.287 |
0.042 |
0.949 |
|
||||
0.763 |
0.623 |
0.049 |
0.949 |
|
|
5. Method 2: Neural Networks
Neural networks consist of simple parallel elements called neurons. Networks are trained on the known pairs of input and output (target) vectors and connections (weights) between the neurons change in such a manner that ensure decreasing a mean difference e between the target and network output. In addition to input and output layers of neurons a network may incorporate one or more hidden layers of computation nodes. To solve difficult pattern recognition problems multilayer feedforward networks or multilayer perceptrons are successfully applied [see 2, 3] since a back-propagation algorithm had been proposed to train them.
The network chosen for the diagnosing has the following structure which is partially determined by the measurement system and fault classification compositions.
The input layer incorporates 6 nodes which correspond to a residual vector dimension. The output layer points to the concerned classes and therefore includes nine elements for the single type classification and four elements for the multiple one. Hidden layer’s structure determines a network complexity and resolution capability. As a first approximation, one hidden layer of 12 nodes has been inserted. In back-propagation networks, layer transfer functions should be differentiable and usually are of sigmoid type. In the hidden layer of the analyzed network, a tan-sigmoid function is applied that varies from - 1 to 1 and is typical for internal layers of a back-propagation network. A log–sigmoid function operates in the output layer; it changes from 0 to 1 and is convenient to solve recognition problems.
Inside a statistical testing procedure, the described network passes training and verification stages. A training algorithm is performed on the reference set
, then the trained network passes a verification stage where the probabilistic trustworthiness indices (see section 3) corresponding to the sets
and
are computed. It is clear that the indices obtained on the testing set are more objective and they will be mostly used an analysis. However, the indices computed on the reference set are useful too because a difference between these two types of indices permits to observe and control the over-teaching effect. The same reference and testing sets, which were used for the method 1, are applied now in order to put the compared methods under equal conditions.
A number of variations exist of a basic back-propagation training algorithm. To choose the best one in conditions of gas turbine fault recognition, twelve variations were tested under the condition of fixed given accuracy e (mean discrepancy between all targets and network outputs) and compared by execution time. Two more perspective algorithms, resilient back-propagation (“rp”-algorithm) and scaled conjugate gradient algorithm (“scg”-algorithm), were verified additionally for the different accuracy levels e = 0.03-0.0275, where the value 0.0275 is close to the final obtainable accuracy. The results given in Table 4 show that the “rp”-algorithm is more rapid while the “scg”-algorithm seems to be a little more reliable on the testing set. Taking into account our priority, recognition trustworthiness, the scaled conjugate gradient algorithm is set for next calculations as a primary algorithm and the resilient back-propagation as a secondary one.
Table 4. Training algorithm comparison.
The word “Epochs” refers to the total epochs number of training process.
and
mean averaged probabilities of truthful diagnosis obtained on the reference and testing sets correspondingly.
e |
Algo-rithm |
Epochs |
Time, s |
|
|
0.0300 |
“rp” |
65 |
37 |
0.8132 |
0.8090 |
“scg” |
111 |
70 |
0.8174 |
0.8172 |
|
0.0290 |
“rp” |
95 |
44 |
0.8168 |
0.8126 |
“scg” |
114 |
71 |
0.8213 |
0.8181 |
|
0.0285 |
“rp” |
118 |
49 |
0.8196 |
0.8149 |
“scg” |
122 |
75 |
0.8209 |
0.8180 |
|
0.0280 |
“rp” |
149 |
56 |
0.8242 |
0.8159 |
“scg” |
134 |
80 |
0.8234 |
0.8214 |
|
0.0275 |
“rp” |
212 |
70 |
0.8269 |
0.8198 |
“scg” |
178 |
100 |
0.8267 |
0.8228 |
Comparing the columns
and
shows that the indices obtained on the reference sample are slightly higher however the difference (
-
) does not exceed the magnitude 0.01. This tendency remains for all other calculations and signifies that the over-teaching effect is practically absent.
An influence of the hidden layer node number was examined too. Above the chosen number 12, the numbers 8, 16, 20 were also probed. The reduction of the node number from 12 to 8 has demonstrated visible changes for the worse of the obtainable accuracy and the probabilities
and
. On the other hand, the augmentation to 16 and 20 nodes has not improved the algorithm’s characteristics. So, the node number 12 does not need to be changed.
6. Methods Comparison
The statistical testing procedure incorporating the described network has been executed for the single and multiple type classifications in the same conditions of method 1 calculations. The probabilities of false diagnosis (5), plotted in Fig. 3 for both methods, help to compare them. It can be seen for every classification that the probabilities of the method 2 are distributed more uniformly and the most of them are lower than the method 1 probabilities. The mean error probability
decreases in this case from 0.2258 to 0.1772 for the single type and from 0.1790 to 0.1293 for the multiple one. These results may be interpreted as a considerable trustworthiness growth of the diagnosing by artificial networks. To ensure the results, the statistical testing procedures of every method were repeated 10 times (option of the single type classification) with different random number series. As a result, average values M(Pe) and standard deviations s(Pe) of the error probabilities have been computed. Analyzing these data placed in Table 5 it can be stated that trustworthiness enhancement for the method 2 (reduction of average values) is much greater than probability’s random variations (standard deviations). The mean error probability decreases here from 0.2340 to 0.1812 i.e. on 22.5%.
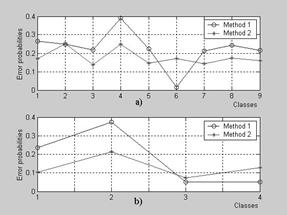
Fig. 3. Probabilities of false diagnosis: a) single type classification; b) multiple type classification
Table 5 Statistical characteristics of the trustworthiness indices
Methods |
Statistics |
|
|
||||||||
D1 |
d2 |
d3 |
d4 |
d5 |
d6 |
d7 |
d8 |
d9 |
|||
1 |
M(Pe) |
0.2834 |
0.2696 |
0.2211 |
0.4231 |
0.2150 |
0.0202 |
0.2223 |
0.2247 |
0.2266 |
0.2340 |
s(Pe) |
0.0174 |
0.0148 |
0.0098 |
0.0312 |
0.0113 |
0.0044 |
0.0131 |
0.0117 |
0.0171 |
0.0041 |
|
2 |
M(Pe) |
0.1602 |
0.2528 |
0.1363 |
0.2649 |
0.1488 |
0.1748 |
0.1542 |
0.1706 |
0.1680 |
0.1812 |
s(Pe) |
0.0144 |
0.0160 |
0.0106 |
0.0186 |
0.0105 |
0.0117 |
0.0123 |
0.0089 |
0.0136 |
0.0032 |
To make the conclusion about network effectiveness more general, in addition to the previous calculations executed for the regime 1 the statistical testing and method comparison were repeated for the other ten operational regimes. The results were very similar: the method 2 always conserved its advantage. Thus, artificial networks may be recommended for feather practical use as a main diagnosing technique.
Executing calculations in different conditions (changes of random numbers and operational regimes) helped to verify more thoroughly the training algorithms. It happened sometimes that the “scg”-algorithm remaining on local minimums could not find the absolute minimum of the error function e. There were the cases where 2000 training epochs were not sufficient to find the solution whereas the normal cycle number is about 200. Unlike described difficulty of the “scg”-algorithm, the “rp”-algorithm always finds the solution.
Fig.4 illustrates a training process of both algorithms on the equal input data. Minimized functions are shown vs. training epochs and the horizontal line means a maximal reachable calculating precision (absolute minimum of error function). As can be seen, the “rp”-algorithm practically finds the solution over normal period of 200 epochs whereas the “scg”-algorithm after the long period of 1000 epochs is still far from the solution. This occurs because the algorithm stays too long in regions of local minimums – horizontal bends in the plot.
Trustworthiness indices corresponding to the described unfinished training are given in Table 6. It can be seen that the vector
includes zero element for the class 5 and the matrix Pd
has a zero line for the same class. One explanation only can be done for this: the fifth network output function remains absolutely untrained after the training. Significant trustworthiness losses result from this. Comparing Table 6 with Table 4, it can be noted that the mean probability of false diagnosis
grew from 0.1812 to 0.2772 i.e. on 50% as a result of bad training. Taking into account given analysis of “scg”-algorithm unreliable work, it was decided to reject this algorithm and accept the resilient back-propagation for further calculations.
The next section describes an attempt to make the classification and the diagnosing process independent on the operational conditions and consequently much more universal.
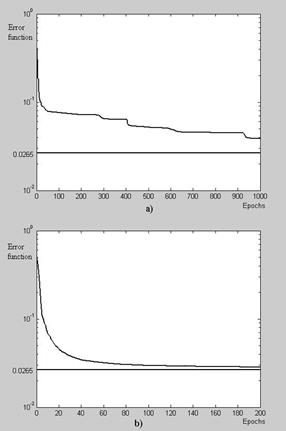
Fig.4. Training behaviour
a) “scg”-algorithm; b) “rp”-algorithm
7. Universal Classification
The executed calculations for different operational regimes have demonstrated a stability of the trustworthiness indices to regime change. A possible reason may be that class presentation in the diagnosing space
is not strongly dependent on operational regime change. Figure 5, which shows the points of maximal fault severity for all 9 classes and 11 regimes, helps to answer this question. It can be seen that the points are grouped according the class number and a regime induced scattering is small. So, class presentation principally depends on specific class and much less on the actual regime.
All these explanations induced the idea to make up the classification that will be independent on operational conditions. In new variants of reference and testing sets, every class incorporates the patterns from all 11 considering regimes. In this case, a region of every class will be more diffused that means greater class intersection and diagnosing trustworthiness losses. However, how much are these losses?
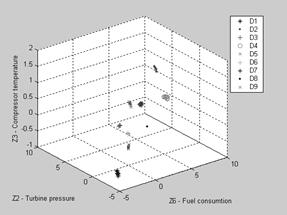
Fig.5. Influence of regime variation on classes’ separability
The statistical testing procedure modified for a new classification helps to quantify a possible negative effect of proposed generalization of the classification. Trustworthiness indices computed by the modified and original procedures for both single and multiple type classifications are given in Table 7. To obtain more precise results, every calculation is executed 10 times with different random number series and average probability values are placed in the table. The data correspond to the testing set. Everyone can note that error probabilities Pej behavior very similarly in the cases of the generalized (all regimes) and common (one regime) classifications and the mean probability
rises just a little, on 0.0055-0.0056.
To sum up this discussion, it can be stated that every class in the generalized classification presents a compact region and is well distinguishable
Table 6. Trustworthiness indices.
Case of the unfinished network training by the “scg”-algorithm
Pd |
|||||||||
Diag-nosis |
Classes |
||||||||
D1 |
D2 |
D3 |
D4 |
D5 |
D6 |
D7 |
D8 |
D9 |
|
d1 |
0.842 |
0.001 |
0.016 |
0.002 |
0.001 |
0.024 |
0.0 |
0.005 |
0.069 |
d2 |
0.0 |
0.735 |
0.0 |
0.155 |
0.048 |
0.006 |
0.006 |
0.003 |
0.0 |
d3 |
0.012 |
0.003 |
0.860 |
0.003 |
0.010 |
0.049 |
0.012 |
0.015 |
0.018 |
d4 |
0.0 |
0.133 |
0.0 |
0.758 |
0.122 |
0.007 |
0.008 |
0.005 |
0.0 |
d5 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
d6 |
0.054 |
0.037 |
0.092 |
0.039 |
0.767 |
0.814 |
0.094 |
0.143 |
0.072 |
d7 |
0.0 |
0.030 |
0.002 |
0.014 |
0.023 |
0.017 |
0.850 |
0.016 |
0.0 |
d8 |
0.005 |
0.053 |
0.023 |
0.028 |
0.027 |
0.061 |
0.027 |
0.807 |
0.002 |
d9 |
0.087 |
0.0 |
0.007 |
0.001 |
0.002 |
0.022 |
0.003 |
0.006 |
0.839 |
|
|||||||||
0.842 |
0.735 |
0.860 |
0.758 |
0.0 |
0.814 |
0.850 |
0.807 |
0.839 |
|
|
Table 7. Diagnosing error probabilities for common and generalized classification
Classi-fication |
Regimes |
M( |
M( |
||||||||
d1 |
d2 |
d3 |
d4 |
d5 |
d6 |
d7 |
d8 |
d9 |
|||
Single |
1 |
0.1657 |
0.2661 |
0.1325 |
0.2652 |
0.1458 |
0.1717 |
0.1545 |
0.1743 |
0.1683 |
0.1827 |
All |
0.1564 |
0.2754 |
0.1309 |
0.2687 |
0.1485 |
0.1898 |
0.1609 |
0.1840 |
0.1803 |
0.1883 |
|
Multiple |
1 |
0.1001 |
0.2049 |
0.0729 |
0.1327 |
- |
- |
- |
- |
- |
0.1276 |
All |
0.1050 |
0.2130 |
0.0761 |
0.1384 |
- |
- |
- |
- |
- |
0.1331 |
8. Conclusions
In this paper, a statistical testing has been discussed of gas turbine diagnosing process in order to determine and elevate recognition trustworthiness indices which are averaged probabilities of true/false diagnosis. A thermodynamic model served to simulate gas turbine degradation modes and form a faults classification.
Two diagnosing methods functioning inside a statistical testing procedure were adjusted, verified, and finally compared. The method applying neural back-propagation networks has demonstrated higher trustworthiness in different conditions of application and is recommended for the use in condition monitoring systems. Inside the total efforts to adjust the network a special attention was paid to choose the best training algorithm and after numerous probes the resilient back-propagation algorithm has been accepted as more reliable and fast.
In made calculations of method comparison, a class representation depended on a gas turbine operational regime, so the classification was regime dependent. This meant in practice a diagnosing on one fixed regime or reconstructing the classification for every new regime. To overcome this difficulty, a generalized classification has been proposed where every class includes patterns from all analyzed regimes. Such a regime independent classification was compared with the original one on basis of the trustworthiness indices and has demonstrated practically the same trustworthiness level. So, without any reliability losses the diagnosing becomes much more universal: the same classification is used for any gas turbine operational conditions.
The paper presented only a part of total work focused on enhancement of gas turbine diagnosing trustworthiness. In addition to described method comparison and classification perfection, numerous investigations were fulfilled by means of a diagnosing process statistical testing and trustworthiness indices analysis in order to study other factors that also affect the gas turbine diagnosing reliability. The variety of these factors includes measurement system structure, measured parameters’ accuracy, diagnosing on dynamic regimes, joint recognition of gaspath faults and measurement system proper defects, and any others.
Presented approach to a trustworthiness problem may be classified as model-based since gas turbine models describe a normal behavior and fault influence. To guarantee the results of model-based calculations the statistical testing is carried out for a wide range of possible diagnosing conditions and the conclusions are generalized. In addition, important results are confirmed on real data, if any.
Acknowledgments
The work has been carried out with the support of the National Polytechnic Institute of Mexico (project 20050709).