Artificial neural networks, fault recognition trustworthiness, fault classification, statistical verification, thermodynamic model.
Abstract — This paper examines an application of artificial neural networks to gas turbine engine diagnosing based on gaspath measured variables. Main focus of the paper is to choose and tune neural networks for diagnostic purposes using trustworthiness indicators. Fault classes are made up from residuals generated by the nonlinear thermodynamic gas turbine model for different gradually developing faults of gas turbine components. The residuals are computed as differences between the measured variables of a faulted engine and a healthy one and also take in account random measurement errors. The trustworthiness indicators present averaged probabilities of gas turbine fault correct recognition. To calculate them, the operation of the neural networks-based diagnostic technique is simulated numerously on different input data, the correct diagnostic decisions are fixed, and corresponding averaged probabilities are computed then. We analysed many variants of network structures and teaching methods and compared them by the trustworthiness indicators. As a result, the optimal network structure and learning method have been chosen. Comparing the artificial neural networks technique with other diagnostic methods, it can be stated that networks application makes gas turbine diagnosis more reliable.
Key words— Artificial neural networks, fault recognition trustworthiness, fault classification, statistical verification, thermodynamic model.
I. INTRODUCTIONThe objectives of a high availability and limiting degradation of gas turbines are very important and many advanced condition monitoring systems are designed and maintained recent years.
As faults of engine components (compressor contamination, turbine erosion, etc.) influence measured and registered gaspath variables (pressures, temperatures, rotation speeds, and so on), there is a theoretical possibility to identify the faults analyzing the measured variables. On the other hand, the changes induced by variations in a gas turbine operational condition are much greater and hide fault effects. In addition, measurement and registration proper errors (random errors, bias, drift) mask the analyzed gaspath faults. So, gas turbine diagnosing presents a challenging recognition problem and raw measurement data should be subjected to a complex mathematical treatment to obtain final result – identified faults of gas turbine components (compressors, combustors, turbines).
Reviewing works on condition monitoring it can be stated that a simulation of gas turbines is an integral part of their diagnostic process [1], [5] and [6]. The main functions of mathematical models in diagnostics are to give a gas turbine performance baseline and to calculate changes in gaspath measurements (fault portraits) induced by different possible faults.
In first gas turbine health monitoring systems, any use of complex statistical recognition methods was too expensive in time and computer capacity. Therefore it was often decided to reduce processing requirements by a diagnostic techniques simplification such as linear models and sign matrixes. Over recent years significant advances in instrumentation and computer technology resulted in more perfect approaches such as the works [6].
The technique proposed in this paper is based on non-linear gaspath model and artificial neural networks. In contrast to many previous investigations, the paper focuses on the trustworthiness problem of gas turbine diagnosing. The following section describes the applied model.
II. Gaspath model
A gas turbine computer model can generate a lot of diagnostic information that would be hard to gather on a real engine.
To operate as a baseline of the gaspath variables
, the model must reflect an influence of the operational condition vector
which includes control variables (fuel consumption and any other) and ambient conditions (air pressure, temperature, and humidity). On the other hand to be capable to simulate gas turbine degradation, the model must take into account a health of every component. For this reason, the vector of correction factors
is introduced into the model in order to displace the maps of component performances and in this way simulate different faults of variable severity. So, the diagnostic gaspath model can be structurally presented by the vector function
.
Used in our investigations non-linear thermodynamic model corresponds to this structure and is computed as a solution of the system of algebraic equations reflecting the conditions of a gas turbine modules combined work. Due to realized objective physical principles the model has a capacity to reflect the normal engine behaviour. Moreover, since the faults affect the module performances involving in the calculations, the thermodynamic model is capable to simulate different mechanisms of gas turbine degradation. The thermodynamic model was developed and all calculations were executed for the two spool free turbine power plant to drive a natural gas compressor set. These calculations included statistical simulation of typical gradually growing gaspath faults in order to make up fault classification.
III. Diagnosing process simulation
In this paper we accept the hypothesis that measured values of gaspath variables
differ from the model generated values only by random measurement errors
i.e.
. (1)
In condition monitoring, instead of measured values
the residuals
are usually applied which present relative changes of gaspath variables
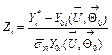, (2)
where
is a base-line value,
- maximal amplitude of random errors.
In contrast to absolute gaspath variables, these residuals do not practically depend on operational condition and serve as good fault indicators. For this reason, we organize the work of our recognition technique and make up a necessary fault classifications just in the space of the residuals. The recognition algorithm operates as follows.
In the classification D1, D2,… Dq
given by a reference set
of the residuals, every class Dj presents a sample
of the residuals corresponding to all possible changes of one correction factor
. An actual change of
is given by an uniform distribution, the gaspath variables are generated by the thermodynamic model next, measured values (1) are calculated then taking into consideration a normal distribution of their errors, and finally, the residuals (2) are determined. A total volume of every statistically generated sample
is
residual vectors (points in the space of residuals). The reference set
is employed to train neural networks of the diagnostic algorithm.
To verify the algorithm and obtain its trustworthiness indices, it is repeated numerously inside of a testing cycle. To be a source of algorithm input data, a testing set
of a volume
is composed in the same way as the reference set is done. An only difference exists – a different random number sequence.
Probabilistic indices
and
are computed during the algorithm statistical testing by the averaging the diagnostic decisions d1, d2,… dq
of the algorithm. Elements of the vector
signify average probabilities of the truthful recognition of the classes. The index
formed as a mean number of these elements characterizes the total controllability of the engine.
IV. Conditions of the statistical testing
The statistical testing of the networks-based recognition algorithm was carried under the following conditions.
Gas turbine steady state operation was determined by a constant compressor rotation speed under standard ambient condition.
Measured variables’ structure corresponded to a gas turbine regular measurement system and included 6 gaspath variables.
The classification consisted of nine classes corresponding to nine correction factors
to be varied: two factors (flow factor and efficiency factor) for every main component (compressor, combustion chamber, compressor turbine, free turbine) and pressure loss factor for an inlet unit. All variations
were uniformly distributed within the interval [0, 5%]. The class probabilities also had a uniform distribution, so every class was equally probable.
There are a lot of neural networks’ types successfully used in different branches of science and we had to choose the most effective one and to adjust it.
V. Neural Networks
Artificial neural networks consist of simple parallel elements called neurons. Networks are trained on the known pairs of input and output (target) vectors and connections (weights) between the neurons change in such a manner that ensure decreasing a mean difference e between the target and network output. In addition to input and output layers of neurons, a network may incorporate one or more hidden layers of computation nodes. To solve difficult pattern recognition problems multilayer feedforward networks or multilayer perceptrons are successfully applied (see [2] and [3]) since a back-propagation algorithm had been proposed to train them.
The network chosen for the diagnosing has the following structure which is partially determined by the measurement system and fault classification compositions.
The input layer incorporates 6 nodes (see Fig.1) which correspond to a measurement vector dimension. The output layer points to the concerned classes and therefore includes nine elements. Hidden layer’s structure determines a network complexity and resolution capability. As a first approximation, one hidden layer of 12 nodes has been inserted. In back-propagation networks, layer transfer functions should be differentiable and usually are of sigmoid type. In the hidden layer of the analyzed network, a tan-sigmoid function is applied that varies from - 1 to 1 and is typical for internal layers of a back-propagation network. A log–sigmoid function operates in the output layer; it changes from 0 to 1 and is convenient to solve recognition problems.
Inside the recognition technique, the described network passes training and verification stages. A training algorithm is performed on the reference set
, then the trained network passes a verification stage where the probabilistic trustworthiness indices
and
(see section 3) corresponding to the sets
and
are computed. It is clear that the index
obtained on the testing set is more objective and it was mostly used an analysis. However, the index
computed on the reference set was useful too because a difference between these two indices permits to control the over-teaching effect.
There are a lot of variations of a basic back-propagation training algorithm. To choose the best one in application to gas turbine fault recognition, twelve variations were tested under the condition of fixed given error e (mean discrepancy between all targets and network outputs) and compared by execution time (see Table 1).
Comparison of the columns
and
shows that the indices obtained on the reference set are slightly higher however the difference (
-
) does not exceed the magnitude 0.01. This tendency signifies that there is no over-teaching effect here. To confirm this conclusion, the calculations were repeated with the option «Early Stopping» which permits to avoid this effect. Comparing new results shown in Table 3 with the previous ones (Table 2), it can be seen that they are very close i.e. the usual training neither tends to the over-teaching no needs the option «Early Stopping».
Calculations executed in different conditions helped to verify more thoroughly both training algorithms. It happened sometimes that the “scg”-algorithm remaining on local minimums could not find the absolute minimum of the error function e. Fig.2 illustrates such a case. Minimized functions of the algorithms are shown vs. training epochs here and the horizontal line means a maximal reachable calculating precision (absolute minimum of error function). As can be seen, the “rp”-algorithm practically finds the solution over normal period of 200 epochs whereas the “scg”-algorithm is still far from the solution after the long period of 1000 epochs. This occurs because the algorithm stays too long in regions of local minimums – horizontal bends in the plot. Taking into account given analysis of “scg”-algorithm unreliable work, it was decided to reject this algorithm and accept the resilient back-propagation for further calculations.
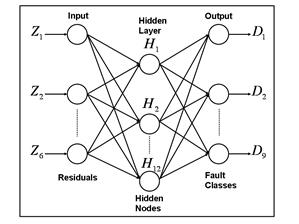Fig.1 Neural network structure
Table 1. Training algorithms
№ |
Algorithm name |
Desig nation |
Points number |
Error e |
Number of epochs |
Execution time, s |
1 |
Levenberg-Marquart |
«LM» |
500 |
0.05 |
30 |
720 |
2 |
Batch Gradient Descent |
«gd» |
500 |
0.05 |
5300 |
420 |
3 |
Batch Gradient Descent with Momentum |
«gdm» |
500 |
0.05 |
5300 |
480 |
4a |
Variable Learning Rate |
«gda» |
500 |
0.05 |
140 |
15 |
4b |
500 |
0.04 |
170 |
- |
||
4c |
500 |
0.03 |
500 |
- |
||
4d |
500 |
0.0275 |
1000 |
- |
||
4e |
500 |
0.0275 |
1000 |
- |
||
4f |
1000 |
0.05 |
190 |
52 |
||
4g |
1000 |
0.0295 |
1000 |
232 |
||
4h |
1000 |
0.03 |
512 |
138 |
||
5 |
«gda»+momentum |
«gdx» |
1000 |
0.03 |
383 |
106 |
6a |
Residual propagation, |
«rp» |
1000 |
0.05 |
24 |
18 |
6b |
1000 |
0.0285 |
1000 |
238 |
||
7 |
Conjugate Gradient, Fletcher-Reeves |
«cgf» |
1000 |
0.053 |
200 |
140 |
8 |
Conjugate Gradient, Polak-Ribiere |
«cgp» |
1000 |
0.0526 |
200 |
120 |
9 |
Conjugate Gradient, Polak-Ribiere |
«cgb» |
1000 |
0.0567 |
200 |
129 |
10a |
Scaled Conjugate Gradient |
«scg» |
1000 |
0.05 |
31 |
32 |
10b |
1000 |
0.0267 |
1000 |
32 |
||
10c |
1000 |
0.04 |
65 |
- |
||
10d |
1000 |
0.03 |
111 |
- |
||
10e |
1000 |
0.027 |
338 |
- |
||
10f |
1000 |
0.028 |
134 |
- |
||
10g |
1000 |
0.029 |
114 |
32 |
||
11 |
Newton Method |
«bgf» |
1000 |
0.0565 |
200 |
130 |
12 |
Quasi Newton Method “One Step Secant” |
«oss» |
1000 |
0.0763 |
200 |
178 |
Table 2. The best training algorithms
Designation |
Error |
Number of epochs |
Time, s |
|
|
|
№6 - “rp” |
0.0275 |
212 |
70 |
0.8269 |
0.8198 |
0.0071 |
№10 – “scg” |
0.0275 |
178 |
100 |
0.8267 |
0.8228 |
0.0039 |
Table 3. Calculations with the «Early Stopping» option
Designation |
Error |
Number of epochs |
Time, s |
|
|
|
№6 - “rp” |
0.02734 |
257 |
108 |
0.8257 |
0.8201 |
0.0056 |
№10 – “scg” |
0.02756 |
168 |
113 |
0.8256 |
0.8220 |
0.0036 |
Table 4. Influence of a hidden layer node number
(algorithm №6 - “rp”, 300 epochs)
n |
Error |
Time, s |
|
|
|
12 |
0.02728 |
90 |
0.8260 |
0.8198 |
0.0062 |
8 |
0.03137 |
77 |
0.8037 |
0.7992 |
0.0045 |
16 |
0.02751 |
102 |
0.8237 |
0.8200 |
0.0037 |
20 |
0.02695 |
115 |
0.8264 |
0.8196 |
0.0068 |
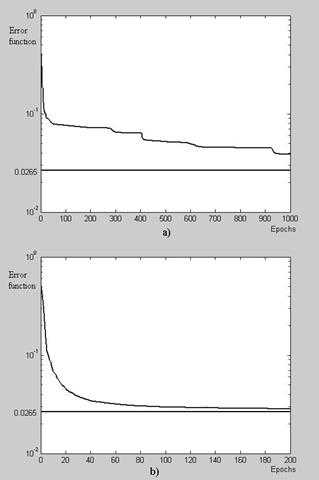
Fig.2. Training behaviour
a) “scg”-algorithm; b) “rp”-algorithm
An influence of the hidden layer node number was examined too. Above the chosen number 12, the numbers 8, 16, 20 were also probed. The reduction of the node number from 12 to 8 has demonstrated visible changes for the worse of the obtainable accuracy and the probabilities
and
.
On the other hand, the augmentations to 16 and 20 nodes have not improved the algorithm’s characteristics. So, the node number 12 was chosen correctly.
After the described stage of statistical testing, the gas turbine recognition technique based on neural networks was preliminary compared with other diagnosing tools we have developed: the method utilizing Bayesian rule [7] and the method applying a geometrical criterion to recognize gas turbine faults [4]. This comparison has shown that neural networks are perspective for a gas turbine diagnosing, however to finally conclude about the best method, the comparative analysis must be more extensive.
VI. Conclusions
In this paper, we described composition and tuning of the gas turbine diagnosing technique on a basis of the artificial neural networks. A nonlinear thermodynamic model served to simulate gas turbine degradation modes and form a faults classification. It is important that the developed technique was statistically tested that permitted to verify it and obtain recognition trustworthiness indices. These indices give a reliability level of the proposed technique and helped to determine structure and parameters of used neural networks.
The neural networks-based diagnosing technique has demonstrated a high trustworthiness level and may be recommended for the practical use in condition monitoring systems. We are working now to compare more thoroughly this technique with other known ones and to surely justify its advantages.
Acknowledgments
The work has been carried out with the support of the National Polytechnic Institute of Mexico (project 20050709).